
Education in the Knowledge Society 22 (2021)

Fuzzy Cognitive Maps and their Application in Social Science Research: A Study of their Main Problems
Los mapas cognitivos difusos y su aplicación en la investigación de las ciencias sociales: estudio de sus principales problemáticas
Alfonso Infante-Moroa, Juan C. Infante-Morob, Julia Gallardo-Pérezc
aDepartamento de Economía Financiera, Contabilidad y Dirección de Operaciones, Universidad de Huelva, Huelva, España.
https://orcid.org/0000-0002-0718-7053alfonso.infante@decd.uhu.es
bDepartamento de Economía Financiera, Contabilidad y Dirección de Operaciones, Universidad de Huelva, Huelva, España.
https://orcid.org/0000-0003-0239-5053juancarlos.infante@decd.uhu.es
cDepartamento de Economía Financiera, Contabilidad y Dirección de Operaciones, Universidad de Huelva, Huelva, España.
https://orcid.org/0000-0002-2227-1835julia.gallardo@decd.uhu.es
ABSTRACT
The methodology of Fuzzy Cognitive Maps (FCMs) is one of the most relevant in the study of knowledge and, probably, one of the most used in recent times by researchers in their studies and projects. This paper analyzes, through a bibliographic review by the main scientific databases, the use of this tool in scientific research and its application in the social sciences, as well as providing historical references in this regard. It shows the main characteristics of the methodology, its possibilities and limitations, its differences with its predecessor (Cognitive Maps), the operational phases for its application and the different ways of capturing information. In addition to demonstrating the suitability of its application in the field of social sciences and studying its major problems, the identification of the concepts involved within the system to be studied, the selection of experts and the coefficients or weights of the knowledge of each of these ones, offering suggestions and contributions for a correct identification of the concepts involved, a correct selection of these experts and a correct quantification of their coefficients of “expert knowledge”.
Keywords:
Research in Social Sciences
Methodologies
Fuzzy Cognitive Maps (FCM)
Cognitive maps
Selection of experts
RESUMEN
La metodología de los Mapas Cognitivos Difusos (MCD) es una de las más relevantes en el estudio del conocimiento y, probablemente, una de las más utilizadas en los últimos tiempos por los investigadores en sus estudios y proyectos. Este artículo analiza a través de una revisión bibliográfica por las principales bases de datos científicas, el uso de esta herramienta en la investigación científica y su aplicación en las ciencias sociales, además de aportar referencias históricas al respecto. Muestra las principales características de la metodología, sus posibilidades y limitaciones, sus diferencias con su antecesor (los Mapas Cognitivos), las fases operativas para su aplicación y las diferentes formas de captación de información. Además de demostrar la idoneidad de su aplicación en el ámbito de las ciencias sociales y estudiar sus mayores problemáticas, la identificación de los conceptos involucrados dentro del sistema a estudiar, la selección de expertos y los coeficientes o pesos de los conocimientos de cada uno de estos, ofreciendo sugerencias y aportaciones para una correcta identificación de los conceptos involucrados, una correcta selección de estos expertos y una correcta cuantificación de sus coeficientes de “conocimiento experto”.
Palabras Clave:
Investigación en Ciencias Sociales
Metodologías
Mapas Cognitivos Difusos (MCD)
Mapas cognitivos
Selección de expertos
1. Introducción
El ámbito de la investigación requiere de métodos y técnicas que aporten resultados relevantes y significativos sobre las áreas investigadas, que da como resultado multitud de estudios en función del fin que se pretenda conseguir (fin exploratorio, descriptivo y/o explicativo) (Ramos Chagoya, 2018). Por ello, podemos observar entre estos estudios: las revisiones literarias (Hernández-Soto, Gutiérrez-Ortega, & Rubia-Avi, 2021; Valencia-Galeano & Serrano-Sánchez, 2020), los bibliométricos (González-Zamar, Abad-Segura, & Gallardo-Pérez, 2021; Abad-Segura, González-Zamar, de la Rosa, & Gallardo-Pérez, 2020), los estudios del caso (Grande-de-Prado, García-Peñalvo, Corell, & Abella-García, 2021; González-González, Gil, Collazos, & González-Calleros, 2021; González-González, Violant Holz, Infante Moro, Cáceres García, & Guzmán Franco, 2021; García-Peñalvo, 2020, 2021), los realizados a través de encuestas (Martínez Pérez, Fernández Robles, & Barroso Osuna, 2021; Infante-Moro, Infante-Moro, & Gallardo-Pérez, 2020d, 2021c; Pozo-Sánchez, López-Belmonte, Fuentes-Cabrera, & López-Núñez, 2021; Pacheco-Cortés & Infante-Moro, 2020) o entrevistas (Sanromà-Giménez, Lázaro Cantabrana, Usart Rodríguez, & Gisbert-Cervera, 2021), y los analizados con estadística (Téllez-Martínez, Cantón-Mayo, & García-Martín, 2021; del Castillo-Olivares & del Castillo-Olivares, 2021) o que siguen metodologías concretas, como Delphi (Infante-Moro, Infante-Moro, & Gallardo-Pérez, 2021a) y/o PLS (Martínez Ávila & Fierro Moreno, 2018), entre otras. En este estudio, centramos el análisis en una de estas metodologías y técnicas, los Mapas Cognitivos Difusos (MCD) y su aplicación en la investigación de las ciencias sociales.
La metodología de los Mapas Cognitivos Difusos (MCD) es una de las más relevantes en el estudio del conocimiento y, probablemente, una de las más utilizadas en los últimos tiempos por los investigadores en sus estudios y proyectos. Una herramienta que se puede utilizar en diferentes situaciones o problemáticas para identificar, definir y validar los constructos o ítems de un sistema e identificar las relaciones causa-efecto que existen entre ellos, con el fin de plantear estrategias y ayudar a la toma de dediciones (Curia & Lavalle, 2011). Además de poder anticiparse a posibles nuevos escenarios por cambios en el comportamiento de alguno de estos constructos.
Así, en el ámbito científico se emplea por su aplicación: descriptiva (para describir un sistema, con los ítems o agentes intervinientes en ese sistema), explicativa (para explicar el por qué del comportamiento de los ítems o agentes intervinientes de un sistema), reflexiva (para tomar decisiones, como instrumento de apoyo a la toma de decisiones) y/o predictiva (para predecir las acciones de los ítems o agentes intervinientes en un sistema) (Codara, 1998).
Estas aplicaciones hacen que sea una herramienta útil para los investigadores de muchas disciplinas científicas: medicina (Saleh, Rivas, Gomez, Mohsen, & Vàzquez, 2016), marketing (Obregón Cabezas & Sánchez Zambrano, 2017), ingeniería (Gil, Aguilar, Dapena, & Rivas, 2018), banca (Castilla Mora, 2017), empresa (Infante-Moro, Infante-Moro, & Gallardo-Pérez, 2021b), educación (Méndez, Calleros, García, Ordóñez, & Lara, 2018) y tecnologías (Vázquez, Teruel, Estrada, & González, 2013), entre otras. Aunque, en este estudio, centramos su análisis en demostrar la idoneidad de su aplicación en el ámbito de las ciencias sociales.
Además, analizamos los puntos claves para la significatividad de la aplicación de esta metodología, que a su vez son sus principales problemáticas: la identificación de los conceptos involucrados dentro del sistema a estudiar, la selección de expertos y los coeficientes o pesos de los conocimientos de cada uno de estos; ofreciendo sugerencias y aportaciones para una correcta identificación de los conceptos involucrados, una correcta selección de estos expertos y una correcta cuantificación de sus coeficientes de “conocimiento experto”.
Para ello, se realiza un estudio bibliográfico a través de las principales bases de datos científicas, revisando lo escrito por los creadores de dicho modelo y los artículos más relevantes en esta metodología, y se reportan referencias, ideas e ítems claves a la hora de demostrar su idoneidad en el ámbito de las ciencias sociales y a la hora de afrontar las problemáticas que pueden afectar a su significatividad.
En la siguiente sección se contextualiza el uso de los Mapas Cognitivos Difusos (MCD) en la investigación científica: describiendo el modelo, haciendo un repaso por el origen y su evolución, y demostrando su idoneidad en los estudios del área de las ciencias sociales. Se continúa con la metodología utilizada en este estudio y el análisis de los resultados, y se concluye con sugerencias y aportaciones para obtener resultados válidos y significativos en el desarrollo de esta metodología en el ámbito de las ciencias sociales.
2. Revisión literaria
Este punto analiza el origen de este modelo y lo describe, muestra sus principales características y posibilidades en la investigación, remarca sus diferencias con otras técnicas con las que tiene similitudes, demuestra la idoneidad de su aplicación en el ámbito de las ciencias sociales y hace referencia a las extensiones que aparecen para eliminar las limitaciones de este.
2.1. Mapas Cognitivos Difusos: origen
El método de los Mapas Cognitivos Difusos (MCD) fue desarrollado por B. Kosko (1986, 1993) en la década de los 80, siendo una evolución de los Mapas Cognitivos de Axelrod (1976) y estando sustentado en la teoría de la Lógica Difusa y la teoría de la Causalidad.
La Causalidad es la relación que se establece entre una causa y su efecto, la relación causa-efecto. Un principio clásico de la filosofía y la ciencia, que afirma que todo hecho tiene una causa, y un principio fundamental en el ámbito de la investigación, que permite prevenir, controlar y dominar un hecho o una situación si conocemos su causa. Se puede hablar de esta relación en cualquier ámbito, entre los que se encuentran: acontecimientos, procesos, producción y/o fenómenos.
Y la Lógica Difusa es un método que proporciona una conclusión clara a partir de una información imprecisa o ambigua, es decir, es el método que permite tomar una decisión a un individuo de forma más convincente desde una información que percibe o recibe de manera no clara (Sánchez, 2016). Sería una lógica multi-valuada que permite valores intermedios (variables difusas) para poder tomar decisiones entre sí/no, verdadero/falso, negro/blanco, caliente/frío…, entre otros.
Lofti A. Zadeh fue el creador de este último concepto que aparece por primera vez en la revista “Information and Crontol” en 1965 (Zadeh, 1965) y que él mismo orienta hacia el concepto que conocemos hoy en día como Lógica Difusa en 1971 (Zadeh, 1971).
Respecto a los Mapas Cognitivos, antecesor del método al que dedicamos dicho artículo, se puede decir que omite la teoría de la Lógica Difusa y solo se sustenta en la teoría de la Causalidad, hasta tal punto que se puede llegar a decir que los Mapas Cognitivos son realmente Mapas Causales, ya que solo son representaciones causales entre los elementos que componen dichos mapas.
Y a diferencia de éste, los Mapas Cognitivos Difusos (MCD) sí que también se sustentan en la teoría de la Lógica Difusa. Este método utilizaría el mismo concepto que los Mapas Cognitivos pero agregándoles las variables difusas (que ya citamos anteriormente, y que serían variables que permiten valores intermedios entre dos opciones extremas). Por tanto, estos mapas cognitivos difusos serían estructuras de grafos difusos que representan razonamiento causal.
2.2. Mapas Cognitivos Difusos: descripción, características y posibilidades en la investigación
Cuando se habla de Mapas Cognitivos Difusos (MCD), se debe comenzar hablando de los Mapas Cognitivos (su metodología antecesora), una metodología que posibilita la representación visual de las ideas, conceptos y/o ítems, que forman un sistema y las relaciones causales que existen entre ellos, todo ello enmarcado en un grafo o esquema.
Una representación visual del conocimiento en forma de mapa que es apoyada por autoras como N. Jones (Jones, Ross, Lynam, Perez, & Leitch, 2011) y K. Langfield-Smith (Langfield-Smith & Wirth, 1992), que sugieren que la mejor forma para que los individuos entiendan lo que les rodea es a través de la construcción de modelos simples en su mente.
Estos mapas cognitivos son grafos dirigidos que están formados por conceptos (nodos) y conexiones causales (arcos) que pueden ir con signo positivo o negativo según incremente o decremente un nodo a otro, o pueden ser ausentes si no existen relaciones causales entre dos nodos.
Pero este modelo, además, admite su representación de manera numérica a través de una matriz de conexión (matriz adyacente) en la que la intercepción de cada par de nodos (conceptos) indica la relación existente entre los mismos.
Hasta ese momento, solo se había hablado de relaciones causales precisas, una misma causa siempre provoca el mismo efecto. Pero en el día a día, esto no suele suceder de esta manera, existen relaciones causales que son imprecisas, no siempre una misma causa provoca el mismo efecto (Sobrino, 2012; Puente, Olivas, & Sobrino, 2010). Por ese mismo motivo, B. Kosko (1986, 1993) hace una evolución de estos Mapas Cognitivos de Axelrod (1976) y desarrolla los Mapas Cognitivos Difusos (MCD), añadiéndoles relaciones causales imprecisas o variables difusas que permitan representar el grado de influencia entre un nodo y otro mediante la lógica difusa, extendiendo su definición a estructuras de grafos difusos que representan razonamiento causal.
Así, este método permite deducir información sobre la importancia de los conceptos implicados en el problema e identificar cuáles son los verdaderamente involucrados en dicha problemática. Un proceso de diseño y ejecución que se divide en tres fases: “Fase de definición”, “Fase de iniciación” y “Fase de ejecución”.
Fase de definición
Fase en la que se analiza el sistema e identifica y define los conceptos involucrados en dicho sistema, cada uno de los conceptos involucrados será representado como uno de los nodos del grafo o matriz que conforma el mapa cognitivo.
Fase de iniciación
Ésta es la fase con más trabajo, es la fase en la que se establecen las relaciones entre los conceptos.
Existen tres maneras diferentes de establecer las relaciones causales entre los conceptos (nodos): “Basándose en la opinión de los expertos”, “Utilizando Mapas Cognitivos Difusos Aumentados” y “Basándose en datos históricos”.
- Basándose en la opinión de los expertos.
En esta forma, se busca explorar la experiencia y el conocimiento. Cada experto define su propio mapa cognitivo difuso y, finalmente, se determina un mapa cognitivo difuso global con los resultados individuales obtenidos.
Lo deseable es que cada uno de los expertos que forme la muestra a analizar realice un dibujo de la red conceptual del sistema a estudiar y las conexiones causales existentes, aunque también se permite en este modelo la obtención de esta información a través de entrevistas o cuestionarios (Özesmi & Özesmi, 2004).
- Utilizando Mapas Cognitivos Difusos Aumentados.
En esta forma, se combinan las matrices de diferentes mapas cognitivos difusos (MCD) de una misma área para formar un nuevo mapa cognitivo difuso (MCD). Si una de estas matrices no incluye un concepto, la fila y columna de éste se rellena con ceros.
- Basándose en datos históricos.
En esta forma, se buscan los datos de entrada en datos del sistema ya medidos anteriormente.
Fase de ejecución
Fase en la que se analiza el sistema a través del mapa cognitivo difuso (MCD).
En esta fase se utiliza algún software de análisis como FCMappers que permite analizar el mapa obtenido y clasificar las variables del sistema según su influencia en el resto de las variables y obtener los indicadores outdegree, indegree y de centralidad (Bachhofer & Wildenberg, 2010).
La clasificación de las variables se realiza en función de la influencia de cada una de ellas en el resto de las variables, y las variables que se pueden encontrar son (Eden, Ackermann, & Cropper, 1992; Bougon, Weick, & Binkhorst, 1977; Harary, Norman, & Cartwright, 1965):
- Variables transmisoras. También llamadas fuerzas o drivers.
- Variables receptoras. También llamadas estados respuestas o productos finales.
- Variables ordinarias. También llamadas medios o factores, que son variables transmisoras y receptoras a la vez.
Y los indicadores que permiten el análisis de la estructura de los mapas cognitivos difusos (MCD) son (Özesmi & Özesmi, 2003):
- El indicador outdegree, que es la suma de los valores de la matriz adyacente asociados con los conectores que salen de un nodo o variable. Una variable transmisora presenta un alto outdegree.
- El indicador indegree, que es la suma de los valores de la matriz adyacente asociados a las conexiones que entran en un nodo. Este indicador muestra el grado de dependencia de la variable. Una variable receptora presenta un alto indegree.
- El indicador de centralidad, que es la suma de los indicadores outdegree e indegree. Este indicador indica el grado de participación o importancia de la variable en el sistema.
2.3. Diferencias con otras técnicas
Con todo esto, esta técnica tiene similitudes con otras metodologías como los “Modelos de Ecuaciones Estructurales (SEM)”, los “Partial Least Squares (PLS)” y los “Sistemas de expertos”, pero estas otras técnicas no tienen los mismos fines que ésta ni las mismas características.
Respecto a los “Modelos de Ecuaciones Estructurales (SEM)”, este modelo permite modelizar relaciones causales entre las variables observadas de un sistema a estudiar y permite agregar nuevas variables, pero sus resultados no son suficientes para la toma de decisiones (De Maio et al., 2015).
Respecto a los “Partial Least Squares (PLS)”, una técnica estadística que permite el análisis del sistema desarrollado por los SEM, pero que solo permite las relaciones unidireccionales. Aunque en poco tiempo, nuevas extensiones en este modelo (como los PLSc) permitirán las relaciones bidireccionales (Roldán Salgueiro & Cepeda Carrión, 2019).
Y respecto a los “Sistemas de expertos”, técnicas que requieren de los conocimientos de los expertos, al igual que los Mapas Cognitivos Difusos (MCD), pero que realizan este proceso de una forma más lenta. Además, los investigadores suelen preferir los Mapas Cognitivos Difusos (MCD) por sus facilidades a la hora de representar el conocimiento y por la posibilidad de que las inferencias puedan realizarse con operaciones matriciales en lugar de con reglas explícitas if/then (Aguilar, 2005).
2.4. Aplicación en investigaciones y estudios de las ciencias sociales
Tal y como se describía en la introducción, esta metodología se ha utilizado por investigadores de diferentes disciplinas científicas: medicina, marketing, ingeniería, banca, empresa, educación y tecnologías, entre otras.
A lo largo de estos más de 30 años desde su creación, se ha consolidado como uno de los modelos más relevantes en el estudio del conocimiento y, este hecho, ha provocado que su uso irrumpiera en una gran variedad de campos -Estudios bibliográficos como los de Aguilar (2005) y Papageorgiou y Salmerón (2013) hacen que podamos visualizar la dispersión científica de esta metodología-. Aunque, en este estudio, centramos su análisis solo en su idoneidad en el área de las ciencias sociales.
Esto último queda demostrado en el número de artículos que utilizan esta metodología en el área y de los que se pueden ver una muestra en los estudios bibliográficos citados en el párrafo anterior. Por tanto, estos Mapas Cognitivos Difusos (MCD) son un modelo aceptado en áreas como la de las ciencias sociales para representar procesos cognitivos a través de un diagrama o grafo. No hay más que decir que R. Axelrod (1976) ya presentó a los Mapas Cognitivos (desde su creación) como una herramienta idónea para representar el conocimiento científico social, una herramienta que permite estructurar un problema, discutirlo con otros y tomar decisiones al respecto.
Así, confirmada la aplicación de esta metodología en el área de las ciencias sociales, resaltar algunos estudios realizados en este área según las cuatro aplicaciones que tienen los Mapas Cognitivos Difusos (MCD) y que nombramos en la introducción: describir sistemas (Dursun & Gumus, 2020; Sánchez, Aguilar, Terán, & de Mesa, 2019; Wang, Liu, Dong, & Soares, 2019), explicar el por qué del comportamiento de los ítems o agentes intervinientes de un sistema (Maden & Alptekin, 2020; Vera-Mora, Leyva-Vásquez, León-Acurio, & Botto-Tobar, 2018; Nayak, Madireddy, Case, & Stylios, 2017), para tomar decisiones (Falcone & De Rosa, 2020; González-González, Infante-Moro, & Infante-Moro, 2020; Salmerón, 2009) y para predecir las acciones de los ítems o agentes intervinientes en un sistema (Liu & Liu, 2020; Ighravwe & Mashao, 2019; Singh, Papageorgiou, Chudasama, & Papageorgiou, 2019). Esta amplitud de aplicaciones demuestra la versatilidad y la gran utilidad de esta metodología en esta área.
Y, además, resaltar su aplicación en una de sus disciplinas, la educación (a la cual pertenece esta revista). En esta disciplina, los Mapas Cognitivos Difusos (MCD) se han empleado con objetivos muy diversos: evaluar el proceso de enseñanza-aprendizaje (Laureano-Cruces, Ramírez-Rodríguez, & Terán-Gilmore, 2004), evaluar la educación (Pacheco, Carlson, & Martins-Pacheco, 2004), modelar software educativo (Hossain & Brooks, 2008), determinar factores críticos en los LMS (Learning Management Systems) (Salmerón, 2009), determinar factores críticos en la implementación de herramientas en los procesos formativos y en las instituciones educativas (Infante-Moro, Infante-Moro, & Gallardo-Pérez, 2020b, 2020c; Infante-Moro, Infante-Moro, Gallardo-Pérez, & Ferreira, 2020), diseñar sistemas de enseñanza (Yu & Qi, 2018; Kao, Lin, & Chu, 2012), diseñar game-based learning y serious games (Luo, Wei, & Zhang, 2009; Cai, Miao, Tan, Shen, & Li, 2010), ajustar la precisión del estilo de aprendizaje (Georgiou & Botsios, 2008), clasificar asignaturas por su importancia en programas de estudio (Solana-Gutiérrez, Rincón-Sanz, Alonso-González, & Bermúdez-Cañete, 2015) o determinar factores relevantes a la hora de que los estudiantes seleccionen universidad para realizar sus estudios (Nayak, Madireddy, Case, & Stylios, 2017). Esta amplitud de aplicaciones demuestra la versatilidad y la gran utilidad de esta metodología en esta disciplina.
2.5. Mapas Cognitivos Difusos: evolución
Como se ha podido observar, los campos de aplicación de los Mapas Cognitivos Difusos (MCD) han ido extendiéndose desde su creación hasta la actualidad, y este proceso no va a detenerse. Las limitaciones de esta metodología y sus subsanaciones son las que han ido marcando y van a seguir marcando su expansión.
Las limitaciones de este modelo son (Papageorgiou & Salmerón, 2013): la introducción del tiempo y el retardo en las interacciones entre conceptos, la linealidad de los pesos de las aristas, la imposibilidad de multiestados en los conceptos, la imposibilidad de modelar sistemas con múltiples significados (grises), la asimetría y el carácter dinámico de algunas relaciones causales, entre otras.
Y los intentos de eliminar dichas limitaciones, han hecho que aparezcan extensiones que mejoran el modelo manteniendo la base de este. Entre estas extensiones se encuentran (Tabla 1):
Tabla 1. Extensiones de la metodología de los Mapas Cognitivos Difusos (MCD).
Rule-Based Fuzzy Cognitive Maps (RBFCM) |
Mapas Cognitivos Difusos Basados en reglas. Esta extensión agrega reglas al modelo tradicional, permitiendo una retroalimentación y herramientas que posibilitan el uso de diferentes relaciones causa-efecto (Carvalho & Tomé, 1999). En 2001, además, agrega la variable tiempo (Carvalho & Tomé, 2001). |
Dynamic Random Fuzzy Cognitive Maps (DRFCM) |
Mapas Cognitivos Difusos aleatorios dinámicos. Esta extensión comienza permitiendo cuantificar la posibilidad de activación de los nodos de un sistema (Aguilar, 2001) y acaba agregándole el carácter dinámico, haciendo posible que las relaciones causales cambien a lo largo del tiempo (Aguilar, 2004). |
Active Hebbian learning algorithm to train Fuzzy Cognitive Maps |
Algoritmo de aprendizaje Hebbiano activo para Mapas Cognitivos Difusos. Esta extensión permite descifrar la secuencia de los nodos de activación (Papageorgiou, Stylios, & Groumpos, 2004). |
Fuzzy Cognitive Maps Learning Using Particle Swarm Optimization |
Aprendizaje en Mapas Cognitivos Difusos usando optimización de enjambre de partículas. Esta extensión permite establecer la matriz idónea para que el sistema consiga alcanzar un equilibrio (Papageorgiou, Parsopoulos, Stylios, Groumpos, & Vrahatis, 2005). |
Fuzzy Cognitive Networks (FCN) |
Redes cognitivas difusas. Esta extensión permite una actualización constante del valor de las relaciones, utilizando también los anteriores puntos de equilibrio del propio mapa como fuente de información para dicha actualización (Kottas, Boutalis, & Christodoulou, 2007). |
Fuzzy Grey Cognitive Maps (FGCM) |
Mapas Cognitivos Difusos grises. Esta extensión permite el estudio de sistemas con significados múltiples, posibilitando el estudio de relaciones casuales expresadas en términos imprecisos (Salmerón, 2010). |
Intuitionistic Fuzzy Cognitive Maps (IFCM) |
Mapas Cognitivos Difusos Intuicionistas. Esta extensión permite calcular el nivel de indecisión de los expertos a la hora de cuantificar las relaciones causa-efecto y hace que el modelo sea menos sensible a la ausencia de datos de entrada (Iakovidis & Papageorgiou, 2011). |
Granular Fuzzy Cognitive Maps (GFCM) |
Mapas Cognitivos Difusos Granulares. Esta extensión agrega el componente error al establecer las conexiones causales (Pedrycz & Homenda, 2014). |
Fuente: (Castilla Mora, 2017).
3. Metodología
Ahora bien, centrándonos en los Mapas Cognitivos Difusos (MCD) y no en sus extensiones, tras hacer un análisis de los pasos a realizar y de los puntos a tener en cuenta a la hora de aplicar dicha metodología, hallamos tres problemáticas que son claves en la significatividad de la aplicación de esta metodología:
- La identificación de los conceptos involucrados dentro del sistema a estudiar, buscando la homogeneidad en los conceptos utilizados en los mapas conceptuales por cada una de las personas que forman la muestra a analizar y evitando la heterogeneidad a la hora definir un mismo concepto, lo que podría desvirtuar el sistema y los resultados alcanzados.
- La selección de expertos, tanto en el número de ellos como en su perfil, ítems relevantes para otorgar credibilidad y significatividad a los resultados que se obtienen.
- Y los coeficientes o pesos de los conocimientos de cada uno de los expertos, buscando los resultados más cercanos a la realidad según el grado de conocimiento del sistema a estudiar por parte de los participantes.
Para ello, se realiza un estudio bibliográfico a través de las principales bases de datos científicas (Web of Science, Scopus y Google Scholar), revisando lo escrito por los creadores de dicho modelo y los artículos más relevantes en esta metodología, y se reportan referencias, ideas e ítems claves a la hora de afrontar las problemáticas que pueden afectar a esta significatividad: ofreciendo sugerencias y aportaciones para una correcta identificación de los conceptos involucrados, una correcta selección de estos expertos y una correcta cuantificación de sus coeficientes de “conocimiento experto”.
Si se hace una búsqueda de esta metodología en las bases de datos citadas anteriormente, Mapa Cognitivo Difuso (MCD) aparece en 2.115 resultados en Web of Science, en 15.795 resultados en Scopus y en 216.000 resultados en Google Scholar.
4. Resultados
Tras la revisión bibliográfica, el análisis de los resultados se hace en base a las tres problemáticas que son claves en la significatividad de la aplicación de esta metodología: la identificación de los conceptos involucrados dentro del sistema a estudiar, la selección de expertos y los coeficientes o pesos de los conocimientos de cada uno de estos.
4.1. La problemática de la identificación de los conceptos involucrados dentro del sistema a estudiar
Una vez presentada la metodología de los Mapas Cognitivos Difusos (MCD) en la revisión literaria se puede observar a simple vista, cuando en la fase de iniciación se utiliza la opinión de los expertos para establecer las relaciones entre los conceptos, que una de sus mayores problemáticas se va a encontrar en la identificación de los conceptos involucrados dentro del sistema a estudiar.
A pesar que en este modelo es deseable que cada una de las personas que formen la muestra a analizar realice un dibujo de la red conceptual del sistema a estudiar sin ninguna guía u orientación y establezca las conexiones causales que existan entre cada uno de los conceptos, se recomienda entregar una plantilla con una serie de variables o componentes sistémicas predefinidas previamente en la fase de definición como los nodos o constructos del sistema a estudiar y una tabla de valoración semántica, cuya graduación semántica de las conexiones se fije en función del grado de influencia causal que cada uno de los expertos piense que una variable pueda tener en otra, y si esa influencia es positiva o negativa (Mouratiadou & Moran, 2007). Este proceso permite conseguir una homogeneidad en los conceptos utilizados en los mapas conceptuales de los expertos, tal y como se hizo en el estudio de J. Solana (Solana Gutiérrez, Rincón Sanz, Alonso González, & Garcia De Jalon Lastra, 2015) en el que se utilizaba los Mapas Cognitivos Difusos (MCD) como técnica de estudio.
Esa plantilla con las variables sistémicas predefinidas debe servir como guía orientativa para los expertos, pero nunca debe considerarse como limitativa. Los expertos pueden aportar, si lo ven oportuno, nuevas variables al sistema.
La identificación de las variables o conceptos involucrados dentro del modelo a estudiar que forman parte de esa plantilla puede convertirse en un proceso engorroso y cuestionado por la introducción de algunos de estos constructos al sistema. Para hacer una correcta identificación, se recomienda utilizar alguno de los siguientes métodos:
- Realizar una revisión literaria.
Realizar una revisión literaria de estudios previos sobre el modelo a estudiar y sobre los factores que pudieran verse involucrados dentro de ese sistema, observando sí ya en esos estudios se dan evidencias que confirmen que algún constructo está involucrado en el mismo.
- Utilizar el método Delphi.
Utilizar el método Delphi para obtener una visión colectiva de expertos en el área del sistema a estudiar que permita identificar los constructos involucrados en el mismo a través del envío de encuestas sucesivas a este grupo de expertos previamente elegidos (Cabero Almenara & Infante Moro, 2014). Este modelo es recomendado si no se dispone de información suficiente sobre un sistema (Reguant Álvarez & Torrado Fonseca, 2016).
- O utilizar el método PLS (Partial Least Squares).
Utilizar el método PLS para identificar y explicar los constructos que provocan que un fenómeno específico (variable dependiente) se produzca (Cepeda Carrión & Roldán Salgueiro, 2004), lo que permite consecuentemente identificar los constructos que forman un sistema concreto. Este modelo también se sustenta en el juicio de expertos.
4.2. La problemática de la selección de expertos
Cuando en la fase de iniciación se utiliza la opinión de los expertos para establecer las relaciones entre los conceptos, otra de las grandes problemáticas se va a encontrar en la selección de expertos, tanto en el número de ellos como en su perfil.
Respecto al número de estos, el tamaño de la muestra es dado por el empleo de gráficas acumulativas del número de nodos nuevos con respecto al número de individuos pertenecientes al grupo de interés muestreado (Özesmi & Özesmi, 2004). Así, el tamaño de la muestra depende de si los nuevos expertos que se van agregando a la muestra van aportando nodos nuevos o no. De este modo, se puedan observar estudios con una muestra de 45 (Carley & Palmquist, 1992), 41 (Infante Moro, 2017), 29 (Carley & Palmquist, 1992), 8 (Infante-Moro, Infante-Moro, & Gallardo-Pérez, 2020a), 7 (Solana Gutiérrez, Rincón Sanz, Alonso González, & García De Jalon Lastra, 2015) y hasta 4 expertos (Amat Abreu, Ortega Tenezaca, & Yaguar Mariño, 2020).
Una vez que se va aumentando el número de expertos entrevistados, el número de nodos nuevos que cada uno de ellos introduce al sistema estudiado se va reduciendo. Hasta el punto en el que nuevos entrevistados no aportan nuevos nodos al sistema (Figura 1). Este hecho indica que el tamaño de la muestra ha alcanzado su tamaño óptimo y correcto.
Figura 1. Proceso de selección del tamaño de la muestra. Fuente: Elaboración propia.
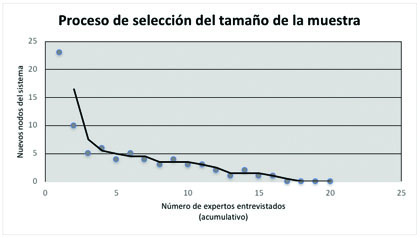
Respecto al perfil de estos, estos expertos deben ser elegidos por el conocimiento, los años de experiencia y la experiencia profesional en el área del sistema a estudiar. Aunque también puede hacerse una selección distinguiendo tipos de expertos (Landeta, 2002): “especialistas” (aquellos que poseen conocimiento científico y experiencia en el área del sistema a estudiar) y “afectados” (aquellos que se encuentran implicados de alguna manera en el área del sistema a estudiar).
Esta selección de expertos es un punto crítico del modelo, ya que la calidad de los resultados depende de los expertos que se utilicen para captar la información necesaria que permita establecer las relaciones entre los conceptos (Papageorgiou & Salmeron, 2014). Por tanto, el perfil de estos siempre ha de quedar remarcado en todo estudio o investigación en la que se utilice esta metodología.
4.3. La problemática de los coeficientes o pesos de los conocimientos de cada uno de los expertos
Y la última de las grandes problemáticas cuando en la fase de iniciación se utiliza la opinión de los expertos para establecer las relaciones entre los conceptos, consiste en la asignación de coeficientes o pesos a los conocimientos de cada uno de estos expertos.
Una muestra puede estar formada por expertos con un perfil similar, en la que la opinión de cada uno de ellos tiene el mismo valor dentro del sistema a estudiar, o por expertos con perfiles dispares, en la que la opinión de cada uno de ellos tiene un valor distinto dentro del sistema a estudiar.
Cuando en la muestra se encuentran distintos perfiles de expertos, es necesario asignar un valor (peso) a los conocimientos de cada uno de ellos. Para este caso, si se quiere conocer la opinión causal entre dos nodos de manera global (englobando la opinión de todos los expertos), se debe utilizar la siguiente ecuación (Aguilar, 2004):
siendo:
NE = Número de expertos
EGji = la opinión global de los expertos e acerca de la relación causal entre dos conceptos: cj y ci
Eeji = la opinión del experto e acerca de la relación causal entre dos conceptos: cj y ci
be = el peso de la credibilidad del experto.
Ahora bien, ¿cuál es el peso que se debe asignar a cada perfil de experto? Esta asignación debe realizarla el investigador en base al conocimiento, a la experiencia y al grado de implicación del experto con el área del sistema a estudiar, y siempre debe quedar justificada en el estudio.
5. Conclusiones
Este artículo pretende hacer un análisis de una de las metodologías más relevantes en el estudio del conocimiento, los Mapas Cognitivos Difusos (MCD). Un análisis que presenta el origen del método, sus características, su desarrollo, su aplicación, su evolución y sus diferencias con algunas de las técnicas con las que más similitudes se encuentra en el mundo de la investigación. Además de ofrecer, como puntos importantes, sugerencias y aportaciones a las principales problemáticas que puede hallar un investigador a la hora de su desarrollo y la idoneidad de su aplicación en el ámbito de las ciencias sociales.
Los Mapas Cognitivos Difusos (MCD) facilitan la visualización de los conceptos o factores que forman un sistema y sus relaciones causa-efecto, lo que permite el estudio de un sistema de una forma más sencilla (Maridueña, Leyva, & Febles, 2016; Papageorgiou, Markinos, & Gemtos, 2009).
Hoy en día, es una de las metodologías más utilizadas en el mundo de la investigación y su aplicación en el mundo científico queda más que demostrada en este artículo, tanto por el número de investigadores que la utilizan en sus estudios como por su dispersión en las distintas áreas del ámbito científico. Mismas razones, que unida a la que ya su creador la presentó como una herramienta idónea para representar el conocimiento científico social, también demuestran la idoneidad a su aplicación en el ámbito de las ciencias sociales (y a una de sus disciplinas, la educación).
Esta técnica se ha utilizado en una gran variedad de fines en este ámbito, lo que permite comprender su utilidad para una diversidad de aplicaciones y temáticas. Aunque si se quieren obtener resultados válidos y significativos en su desarrollo, es necesario seguir las sugerencias y aportaciones de este artículo a las principales problemáticas que puede encontrar un investigador en su desarrollo: la identificación de los conceptos involucrados dentro del sistema a estudiar, la selección de expertos y los coeficientes o pesos de los conocimientos de cada uno de estos, permitiendo una correcta identificación de los conceptos involucrados, una correcta selección de estos expertos y una correcta cuantificación de sus coeficientes de “conocimiento experto”.
Entre estas sugerencias y recomendaciones se encuentran: uso de una revisión literaria, del método Delphi o del método PLS (Partial Least Squares) para la identificación de las variables o conceptos involucrados dentro del sistema a estudiar; emplear gráficas acumulativas del número de nodos nuevos con respecto al número de individuos pertenecientes al grupo de interés muestreado para cuantificar el tamaño de la muestra; elegir a los expertos por el conocimiento, los años de experiencia y la experiencia profesional en el área del sistema a estudiar, o por estar implicados de alguna manera en el área del sistema a estudiar; tener precaución en la selección de los expertos (aplicar para ello los biogramas y el coeficiente de competencia experta); y justificar el valor (peso) a los conocimientos de cada uno de los expertos cuando en la muestra se encuentran distintos perfiles de expertos, justificar en base al conocimiento, a la experiencia y al grado de implicación del experto con el área del sistema a estudiar.
6. Referencias
Abad-Segura, E., González-Zamar, M. D., de la Rosa, A. L., & Gallardo-Pérez, J. (2020). Gestión de la economía digital en la educación superior: tendencias y perspectivas futuras. Campus Virtuales, 9(1), 57–68.
Aguilar, J. (2001). A fuzzy cognitive map based on the random neural model. In L. Monostori, J. Váncza, & M. Ali (Eds.), Engineering of Intelligent Systems (pp. 333–338). Springer https://doi.org/10.1007/3-540-45517-5_37
Aguilar, J. (2004). Dynamic random fuzzy cognitive maps. Revista Computación y Sistemas, 7(4), 260–271.
Aguilar, J. (2005). A survey about fuzzy cognitive maps papers. International Journal of Computational Cognition, 3, 27–33.
Amat Abreu, M., Ortega Tenezaca, D. B., & Yaguar Mariño, J. J. (2020). Determinación del grado de influencia de los factores climáticos de vulnerabilidad del sector agropecuario con técnicas neutrosóficas. Investigación Operacional, 41(5), 699–705.
Axelrod, R. (1976). The Structure of Decision: Cognitive Maps of Political Elites. Princeton University Press.
Bachhofer, M., & Wildenberg, M. (2010). FCMappers. http://www.fcmappers.net
Bougon, M., Weick, K., & Binkhorst, D. (1977). Cognition in organizations: an analysis of the Utrecht Jazz Orchestra. Administrative Science Quarterly, 22, 606–639. https://doi.org/10.2307/2392403
Cabero Almenara, J., & Infante Moro, A. (2014). Empleo del método Delphi y su empleo en la investigación en comunicación y educación. Edutec, 48, 1–16. https://doi.org/10.21556/edutec.2014.48.187
Cai, Y., Miao, C., Tan, A. H., Shen, Z., & Li, B. (2010). Creating an immersive game world with evolutionary fuzzy cognitive maps. IEEE Computer Graphics and Applications, 30(2), 58–70. https://doi.org/10.1109/MCG.2009.80
Carley, K., & Palmquist, M. (1992). Extracting, representing, and analyzing mental models. Social forces, 70(3), 601–636. https://doi.org/10.1093/sf/70.3.601
Carvalho, J., & Tomé, J. (1999). Rule based fuzzy cognitive maps-fuzzy causal relations. In M. Mohammadian (Ed.), Computational Intelligence for Modelling, Control and Automation.
Carvalho, J., & Tomé, J. (2001). Rule based fuzzy cognitive maps-expressing time in qualitative system dynamics. In The 10th IEEE International Conference on Fuzzy Systems (pp. 280–283). IEEE. https://doi.org/10.1109/FUZZ.2001.1007303
Castilla Mora, L. (2017). Percepción de los usuarios sobre el sector financiero español tras la crisis: análisis de la situación con mapas cognitivos difusos. (Doctoral thesis). Universidad de Huelva, Spain.
Cepeda Carrión, G., & Roldán Salgueiro, J. L. (2004). Aplicando en la práctica la técnica PLS en la Administración de Empresas. In Conocimiento y Competitividad: Congreso ACEDE.
Codara L. (1998). Le mappe cognitive. Carocci Editore.
Curia, L., & Lavalle, A. (2011). Estrategias de decisión en sistemas dinámicos- aplicando mapas cognitivos difusos aplicación a un ejemplo socio-económico. JISTEM-Journal of Information Systems and Technology Management, 8(3), 663–680. https://doi.org/10.4301/S1807-17752011000300008
De Maio, C., Botti, A., Fenza, G., Loia, V. T., Troisi, O., & Vesci, M. (2015). What-if analysis combining fuzzy cognitive map and structural equation modeling. In Conference on Technologies and Applications of Artificial Intelligence (TAAI) (pp. 89–96). IEEE. https://doi.org/10.1109/TAAI.2015.7407094
del Castillo-Olivares, J. M., & del Castillo-Olivares, A. (2021). El impacto de la COVID-19 en el profesorado de educación superior y sus concepciones sobre la evaluación. Campus Virtuales, 10(1), 89–101.
Dursun, M., & Gumus, G. (2020). Intuitionistic fuzzy cognitive map approach for the evaluation of supply chain configuration criteria. Mathematical Methods in the Applied Sciences, 43(13), 7788–7801. https://doi.org/10.1002/mma.6238
Eden, C., Ackermann, F., & Cropper, S. (1992). The analysis of cause maps. Journal of Management Studies, 29(3), 309–324. https://doi.org/10.1111/j.1467-6486.1992.tb00667.x
Falcone, P. M., & De Rosa, S. P. (2020). Use of fuzzy cognitive maps to develop policy strategies for the optimization of municipal waste management: A case study of the land of fires (Italy). Land Use Policy, 96, 104680. https://doi.org/10.1016/j.landusepol.2020.104680
García-Peñalvo, F. J. (2020). Modelo de referencia para la enseñanza no presencial en universidades presenciales. Campus Virtuales, 9(1), 41–56.
García-Peñalvo, F. J. (2021). Avoiding the dark side of digital transformation in teaching. An institutional reference framework for eLearning in higher education. Sustainability, 13(4), Article 2023. https://doi.org/10.3390/su13042023
Georgiou, D. A., & Botsios, S. D. (2008). Learning style recognition: A three layers fuzzy cognitive map schema. In 2008 IEEE international conference on fuzzy systems (IEEE World Congress on Computational Intelligence) (pp. 2202–2207). IEEE. https://doi.org/10.1109/FUZZY.2008.4630675
Gil, A., Aguilar, J., Dapena, E., & Rivas, R. (2018). Verification of the emergence in an architecture for multi-robot systems (AMEB). Latin American Journal of Computing Faculty of Systems Engineering Escuela Politécnica Nacional Quito-Ecuador, 5(2), 41–52.
González-González, C. S., Gil, R. M., Collazos, C. A., & González-Calleros, J. M. (2021). Análisis de las titulaciones formales e informales en Iberoamérica de UX: desafíos para la formación online. Campus Virtuales, 10(1), 141–151.
González-González, C. S., Infante-Moro, A., & Infante-Moro, J. C. (2020). Implementation of E-proctoring in online teaching: A study about motivational factors. Sustainability, 12(8), 3488. https://doi.org/10.3390/su12083488
González-González, C. S., Violant Holz, V., Infante Moro, A., Cáceres García, L., & Guzmán Franco, M. D. (2021). Educational robotics in inclusive contexts: The case of the hospital classrooms. Educacion XX1, 24(1), 375–403. https://doi.org/10.5944/educxx1.27047
González-Zamar, M. D., Abad-Segura, E., & Gallardo-Pérez, J. (2021). Aprendizaje ubicuo en educación artística y lenguajes visuales: Análisis de tendencias. Campus Virtuales, 10(1), 125–139.
Grande-de-Prado, M., García-Peñalvo, F. J., Corell Almuzara, A., & Abella-García, V. (2021). Evaluación en Educación Superior durante la pandemia de la COVID-19. Campus Virtuales, 10(1), 49–58.
Harary, F., Norman, R. Z., & Cartwright, D. (1965). Structural Models: An Introduction to the Theory of Directed Graphs. John Wiley & Sons.
Hernández-Soto, R., Gutiérrez-Ortega, M., & Rubia-Avi, B. (2021). Key factors in knowledge sharing behavior in virtual communities of practice: A systematic review. Education in the Knowledge Society, 22(1), e22715. https://doi.org/10.14201/eks.22715
Hossain, S., & Brooks, L. (2008). Fuzzy cognitive map modelling educational software adoption. Computers & Education, 51(4), 1569–1588. https://doi.org/10.1016/j.compedu.2008.03.002
Iakovidis, D., & Papageorgiou, E. (2011). Intuitionistic fuzzy cognitive maps for medical decision making. IEEE Transactions on Information Technology in Biomedicine, 15(1), 100–107. https://doi.org/10.1109/TITB.2010.2093603
Ighravwe, D. E., & Mashao, D. (2019). Predicting energy theft under uncertainty conditions: A fuzzy cognitive maps approach: Energy theft prediction. In 2019 6th International Conference on Soft Computing & Machine Intelligence (ISCMI) (pp. 83–89). IEEE. https://doi.org/10.1109/ISCMI47871.2019.9004344
Infante Moro, J. C. (2017). Percepción de los usuarios para la mejora del uso de las Redes Sociales como canal de comunicación en el sector hotelero. (Doctoral thesis). Universidad de Huelva, Spain.
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2020a). Factores motivacionales que justifican la implementación del Internet de las Cosas como sistema de seguridad en el sector hotelero. Revista de Pensamiento Estratégico y Seguridad CISDE, 5(2), 81–91.
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2020b). Key factors in the implementation of Cloud Computing as a service and communication tool in universities. In Eighth International Conference on Technological Ecosystems for Enhancing Multiculturality (pp. 365–370). ACM International Conference Proceeding Series. https://doi.org/10.1145/3434780.3436698
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2020c). Motivational factors in the insertion of digital skills in teaching. In Eighth International Conference on Technological Ecosystems for Enhancing Multiculturality (pp. 365–370). ACM International Conference Proceeding Series. https://doi.org/10.1145/3434780.3436631
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2020d). Las posibilidades de empleo del Internet de las Cosas en el sector hotelero y sus necesidades formativas. Education in the knowledge society, 21. https://doi.org/10.14201/eks.22777
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2021a). Factores que influyen en la adopción del Internet de las Cosas en el sector hotelero. RISTI - Revista Iberica de Sistemas e Tecnologias de Informacao, (E41), 370–383.
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2021b). Key factors in the implementation of the internet of things in the hotel sector. Applied Sciences, 11(7), 2924. https://doi.org/10.3390/app11072924
Infante-Moro, A., Infante-Moro, J. C., & Gallardo-Pérez, J. (2021c). The acquisition of ICT skills at the university level: The case of the Faculty of Business Studies and Tourism of the University of Huelva. Pixel-Bit, Revista de Medios y Educacion, (60). https://doi.org/10.12795/pixelbit.79471
Infante-Moro, A., Infante-Moro, J. C., Gallardo-Pérez, J., & Ferreira, L. S. (2020). Motivational factors in the insertion of Cloud Computing in teaching. In 2020 X International Conference on Virtual Campus (JICV) (pp. 1–5). IEEE. https://doi.org/10.1109/JICV51605.2020.9375710
Jones, N., Ross, H., Lynam, T., Perez, P., & Leitch, A. (2011). Mental models: An interdisciplinary synthesis of theory and methods. Ecology and Society, 16(1). https://doi.org/10.5751/ES-03802-160146
Kao, Y. T., Lin, Y. S., & Chu, C. P. (2012). A multi-factor fuzzy inference and concept map approach for developing diagnostic and adaptive remedial learning systems. Procedia-Social and Behavioral Sciences, 64, 65–74. https://doi.org/10.1016/j.sbspro.2012.11.009
Kosko, B. (1986). Fuzzy cognitive maps. International Journal of Man-Machine Studies, 24(1), 65–75. https://doi.org/10.1016/S0020-7373(86)80040-2
Kosko, B. (1993). Fuzzy Thinking. The New Science of Fuzzy Logic. Hyperion.
Kottas, T., Boutalis, Y., & Christodoulou, M. (2007). Fuzzy cognitive network: A general framework. Intelligent Decision Technologies, 1(4), 183–196. https://doi.org/10.3233/IDT-2007-1402
Landeta, J. (2002). El método Delphi: una técnica de previsión para la incertidumbre. Ariel.
Langfield-Smith, K., & Wirth, A. (1992). Measuring differences between cognitive maps. Journal of the Operational Research Society, 43(12), 1135–1150. https://doi.org/10.1057/jors.1992.180
Laureano-Cruces, A. L., Ramírez-Rodríguez, J., & Terán-Gilmore, A. (2004). Evaluation of the teaching-learning process with fuzzy cognitive maps. In Ibero-American Conference on Artificial Intelligence (pp. 922–931). Springer. https://doi.org/10.1007/978-3-540-30498-2_92
Liu, Z., & Liu, J. (2020). A robust time series prediction method based on empirical mode decomposition and high-order fuzzy cognitive maps. Knowledge-Based Systems, 203, 106105. https://doi.org/10.1016/j.knosys.2020.106105
Luo, X., Wei, X., & Zhang, J. (2009). Game-based learning model using fuzzy cognitive map. In Proceedings of the First ACM International Workshop on Multimedia Technologies for Distance Learning (pp. 67–76). ACM. https://doi.org/10.1145/1631111.1631123
Maden, A., & Alptekin, E. (2020). Understanding the blockchain technology adoption from procurement professionals’ perspective-an analysis of the technology acceptance model using intuitionistic fuzzy cognitive maps. In International Conference on Intelligent and Fuzzy Systems (pp. 347–354). Springer. https://doi.org/10.1007/978-3-030-51156-2_41
Maridueña, M. R., Leyva, M., & Febles, A. (2016). Modelado y análisis de indicadores de ciencia y tecnología mediante mapas cognitivos difusos. Ciencias de la Información, 47(1), 17–24.
Martínez Ávila, M., & Fierro Moreno, E. (2018). Aplicación de la técnica PLS-SEM en la gestión del conocimiento: un enfoque técnico práctico. RIDE. Revista Iberoamericana para la Investigación y el Desarrollo Educativo, 8(16), 130–164. https://doi.org/10.23913/ride.v8i16.336
Martínez Pérez, S., Fernández Robles, B., & Barroso Osuna, J. (2021). La realidad aumentada como recurso para la formación en la educación superior. Campus Virtuales, 10(1), 9–19.
Méndez, B. E. P., Calleros, J. M. G., García, J. G., Ordóñez, C. A. C., & Lara, A. A. L. (2018). Propuesta de un Tutor Cognitivo semi-automatizado con gamificación e interfaces tangibles para álgebra. Campus Virtuales, 7(1), 63–80.
Mouratiadou, I., & Moran, D. (2007). Mapping public participation in the Water Framework Directive: A case study of the Pinios River Basin, Greece. Ecological economics, 62(1), 66–76. https://doi.org/10.1016/j.ecolecon.2007.01.009
Nayak, P., Madireddy, S., Case, D. M., & Stylios, C. D. (2017). Using fuzzy cognitive maps to model university desirability and selection. In 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC) (pp. 1976–1981). IEEE. https://doi.org/10.1109/SMC.2017.8122908
Obregón Cabezas, F. M., & Sánchez Zambrano, P. A. (2017). Aplicación de Mapas Cognitivos Difusos para la Toma de Decisiones en el Marketing Político-electoral en la Elección de Representantes Estudiantiles de la Universidad de Guayaquil. (Doctoral thesis). Universidad De Guayaquil, Ecuador.
Özesmi, U., & Özesmi, S. L. (2003). A participatory approach to ecosystem conservation: Fuzzy cognitive maps and stakeholder group analysis in Uluabat Lake, Turkey. Environmental management, 31(4), 0518–0531. https://doi.org/10.1007/s00267-002-2841-1
Özesmi, U., & Özesmi, S. L. (2004). Ecological models based on people’s knowledge: A multistep Fuzzy Cognitive Mapping approach. Ecological modelling, 176(1), 43–64. https://doi.org/10.1016/j.ecolmodel.2003.10.027
Pacheco, R. L., Carlson, R., & Martins-Pacheco, L. H. (2004). Engineering education assessment system using fuzzy cognitive maps. Age, 9, 1.
Pacheco-Cortés, A. M.; Infante-Moro, A. (2020). La resignificación de las TIC en un ambiente virtual de aprendizaje. Campus Virtuales, 9(1), 85–99.
Papageorgiou, E. I., Markinos, A. T., & Gemtos, T. (2009). Application of fuzzy cognitive maps for cotton yield management in precision farming. Expert Systems with Applications, 36(10), 12399–12413. https://doi.org/10.1016/j.eswa.2009.04.046
Papageorgiou, E.I., Parsopoulos, K., Stylios, C., Groumpos, P., & Vrahatis, M. (2005). Fuzzy cognitive maps learning using particle swarm optimization. Journal of Intelligent Information Systems, 25(1), 95–121. https://doi.org/10.1007/s10844-005-0864-9
Papageorgiou, E. I., & Salmerón, J. L. (2013). A review of fuzzy cognitive maps research during the last decade. IEEE Transactions on Fuzzy Systems, 21(1), 66–79. https://doi.org/10.1109/TFUZZ.2012.2201727
Papageorgiou, E. I., & Salmeron, J. L. (2014). Methods and algorithms for fuzzy cognitive map-based modeling. In Fuzzy Cognitive Maps for Applied Sciences and Engineering (pp. 1–28). Springer. https://doi.org/10.1007/978-3-642-39739-4_1
Papageorgiou, E., Stylios, C., & Groumpos, P. (2004). Active Hebbian learning algorithm to train fuzzy cognitive maps. International Journal of Approximate Reasoning, 37(3), 219–249. https://doi.org/10.1016/j.ijar.2004.01.001
Pedrycz, W., & Homenda, W. (2014). From fuzzy cognitive maps to granular cognitive maps. IEEE Transactions on Fuzzy Systems, 22(4), 859–869. https://doi.org/10.1109/TFUZZ.2013.2277730
Pozo-Sánchez, S., López-Belmonte, J., Fuentes-Cabrera, A., & López-Núñez, J. A. (2021). Aplicación trietápica del flipped learning en el área de las ciencias. Campus Virtuales, 10(1), 35–47.
Puente, C., Olivas, J. A., & Sobrino, A. (2010). Estudio de las relaciones causales. Anales de mecánica y electricidad, (87), 54–59.
Ramos Chagoya, E. (2018). Métodos y técnicas de investigación. https://www.gestiopolis.com/metodos-y-tecnicas-de-investigacion/
Reguant Álvarez, M., & Torrado Fonseca, M. (2016). El método Delphi. REIRE. Revista d’Innovació i Recerca en Educació, 9(2), 87–102. https://doi.org/10.1344/reire2016.9.1916
Roldán Salgueiro, J. L., & Cepeda Carrión, G. (2019). Modelos de Ecuaciones Estructurales basados en la Varianza: Partial Least Squares (PLS). Módulo 1: Fundamentos básicos.
Saleh, S. H., Rivas, S. D. L., Gomez, A. M. M., Mohsen, F. S., & Vàzquez, M. L. (2016). Representación del conocimiento mediante mapas cognitivos difusos y conjuntos de términos lingüísticos difusos dudosos en la biomedicina. International Journal of Innovation and Applied Studies, 17(1), 312.
Salmerón, J. L. (2009). Supporting decision makers with fuzzy cognitive maps. Research-Technology Management, 52(3), 53–59. https://doi.org/10.1080/08956308.2009.11657569
Salmerón, J. L. (2010). Modelling grey uncertainty with fuzzy grey cognitive maps. Expert Systems with Applications, 37(12), 7581–7588. https://doi.org/10.1016/j.eswa.2010.04.085
Sánchez, H., Aguilar, J., Terán, O., & de Mesa, J. G. (2019). Modeling the process of shaping the public opinion through multilevel fuzzy cognitive maps. Applied Soft Computing, 85, 105756. https://doi.org/10.1016/j.asoc.2019.105756
Sánchez, R. (2016). Lógica difusa. Universidad Carlos III de Madrid.
Sanromà-Giménez, M., Lázaro Cantabrana, J., Usart Rodríguez, M., & Gisbert-Cervera, M. (2021). Design and validation of an assessment tool for educational mobile applications used with autistic learners. Journal of New Approaches in Educational Research, 10(1), 101–121. https://doi.org/10.7821/naer.2021.1.574
Singh, P. K., Papageorgiou, K., Chudasama, H., & Papageorgiou, E. I. (2019). Evaluating the effectiveness of climate change adaptations in the world’s largest mangrove ecosystem. Sustainability, 11(23), 6655. https://doi.org/10.3390/su11236655
Sobrino, A. (2012). Imperfect causality: Combining experimentation and theory. In Combining Experimentation and Theory (pp. 371–389). Springer. https://doi.org/10.1007/978-3-642-24666-1_25
Solana-Gutiérrez, J., Rincón-Sanz, G., Alonso-González, C., & Bermúdez-Cañete, M. P. A. (2015). Using fuzzy cognitive maps for selecting complementary subjects in a professional accredited Master – Master in Forestry Engineering. In INTED2014 Proceedings.
Solana-Gutiérrez, J., Rincón-Sanz, G., Alonso-González, C., & Garcia De Jalon Lastra, D. (2015). Utilización de Mapas de Conocimiento Difuso (MCD) en la asignación de prioridades de la restauración fluvial: Aplicación al río Esla. Cuadernos de la Sociedad Española de Ciencias Forestales, 41, 367–380. https://doi.org/10.31167/csef.v0i41.17402
Téllez-Martínez, S., Cantón-Mayo, I., & García-Martín, S. (2021). Impedimentos a la consecución de la satisfacción y el bienestar docente. Campus Virtuales, 10(1), 185–193.
Valencia-Galeano, Y. S., & Serrano-Sánchez, J. L. (2020). Aprendizaje de un segundo idioma apoyado en tecnologías digitales: una revisión sistemática. Education in the Knowledge Society, 21, 13. https://doi.org/10.14201/eks.18734
Vázquez, M. Y. L., Teruel, K. P., Estrada, A. F., & González, J. G. (2013). Mapas cognitivos difusos para la selección de proyectos de tecnologías de la información. Contaduría y administración, 58(4), 95–117. https://doi.org/10.1016/S0186-1042(13)71235-X
Vera-Mora, G., Leyva-Vásquez, M., León-Acurio, J., & Botto-Tobar, M. (2018). Fuzzy cognitive maps for the analysis of mental models. Revista Espacios, 39(15).
Wang, L., Liu, Q., Dong, S., & Soares, C. G. (2019). Effectiveness assessment of ship navigation safety countermeasures using fuzzy cognitive maps. Safety science, 117, 352–364. https://doi.org/10.1016/j.ssci.2019.04.027
Yu, Y., & Qi, A. (2018). Teaching system of smart learning environment for aerobics course. International Journal of Emerging Technologies in Learning (IJET), 13(05), 165–176. https://doi.org/10.3991/ijet.v13i05.8440
Zadeh, L. A. (1965). Fuzzy set. Information and Control, 8, 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
Zadeh, L. A. (1971). Quantitative fuzzy semantics. Information sciences, 3(2), 159–176. https://doi.org/10.1016/S0020-0255(71)80004-X