Diseño y mejora de actividades de iniciación al pensamiento computacional en el aula de matemáticas

El Real Decreto 157/2022 incluye estas destrezas dentro de la cuarta competencia específica de matemáticas, que va enfocada al propio pensamiento computacional. A su vez, la sexta competencia específica nos habla de la comunicación y la representación de resultados, ya sea de manera oral, escrita o gráfica, para dar significado a las ideas matemáticas que se aprenden. En esta propuesta, el alumnado debía exponer de manera conjunta no solo los resultados de sus experiencias, sino también sus emociones, actitudes y creencias sobre las matemáticas. La octava competencia específica habla del trabajo en equipo, del desarrollo de destrezas sociales y la creación de relaciones saludables. Durante las actividades podían gestionar roles, respetar los turnos de palabra y escuchar distintas ideas de resolución.

Durante la primera sesión (Tabla 1), tras introducir al alumnado en la narrativa de UMASA, se les dejó indagar con la máquina para que se familiarizaran con la misma y su funcionamiento. Tras unos 20 minutos, se introdujeron dos actividades sencillas para completar y crear caminos.

No se especifican las destrezas esperadas en la introducción a la máquina, ya que, aparte de la organización y el análisis de datos, cada pareja podía afrontar la situación de una manera única. Así, algunas duplas empezaron a poner piezas de una en una y fueron testeando poco a poco, otras parejas pusieron más piezas de las necesarias, quitando aquellas que no servían. Cada acción era válida en esta primera parte y solo se esperaba el reconocimiento de la máquina.

Durante la segunda sesión (Tabla 2) se continuaba con tareas de creación de algoritmos. Tras la sesión de iniciación se tenían evidencias que mostraban la diversidad del grupo clase. Para adaptar las siguientes sesiones a los distintos niveles, se diseñaron tres versiones de la misma tarea con tres niveles de dificultad. El alumnado era ajeno a estas diferencias, denominando con eufemismos los ejercicios entregados y repartidos, en apariencia, de forma aleatoria. Se codificó como ejercicios estrella fugaz para tareas del nivel más básico, ejercicios planeta para el nivel intermedio y ejercicios cometa para el nivel más avanzado.

Como se puede apreciar en la Tabla 2, salvo la Tarea 2.4, el enunciado fue el mismo para los tres niveles. Lo único que cambiaba era la disposición de los elementos en el tablero, añadiendo piezas para facilitar la creación del camino o quitándolas para añadir dificultad. La principal destreza que se esperaba desarrollar en esta sesión era la de crear caminos (crear algoritmos).

La tercera sesión (Tabla 3) se centró en el testeo y la depuración de caminos completos que se les presentaba al alumnado. La sesión se separó en dos partes. En una primera se buscaba que el alumnado predijera el resultado tras recorrer un camino completo (ejecutar el algoritmo) y en otra necesitaban optimizar el camino quitando piezas que no afectaban al resultado o detectando elementos del camino que causaban problemas en el resultado.

En esta sesión, para conseguir la adaptación a la diversidad del grupo, se secuenciaron las tareas por dificultad, de forma que cada dupla o trío podía avanzar de manera independiente por las distintas tareas. La generalización provino de reconocer soluciones a partir de tareas previas o al dejar piezas que compartían disposición entre tareas. La creación de algoritmos surgió cuando el alumnado acababa los caminos incompletos que daban problemas.

En la sesión 4 se evaluaba el aprendizaje y se afianzaban destrezas mediante una combinación de tareas, en las que se pedía predecir resultados y crear caminos (Tabla 4). Tras el desarrollo de las sesiones anteriores, se empezó por actividades de predicción, dejando las tareas de crear algoritmos para el final, que resultaron ser más complicadas para el alumnado.

Las sesiones 1, 2 y 3 fueron grabadas, utilizando un equipo de grabación para cada dos grupos de estudiantes. En cada sesión participaron entre 6-7 personas del equipo de investigación, que solo facilitaban documentos con las tareas, en modo de ficha, y grababan. El grupo clase era guiado por una persona del equipo de investigación, que asumía el rol de líder de la misión y docente. En la sesión 4, se escogieron varias parejas de control para grabar en forma de entrevista semiestructurada las actividades (Tabla 4), efectuándoles preguntas en las que se pretendía confirmar el nivel de las actividades, las destrezas desarrolladas y la conexión entre el PC y las matemáticas.

4. Análisis y resultados

4.1. Análisis de datos

Para estudiar el protocolo llevado a cabo, su posibilidad de réplica en otros grupos-clase y mejorar sus pasos, se presenta aquí el análisis de algunas de las grabaciones. La sesión 1, debido a la novedad del tipo de intervención, la contextualización en UMASA, el considerar la actividad como un juego y observando la facilidad con que el alumnado realizaba las tareas, se puede considerar un éxito. Se consiguió una motivación general y la iniciación a determinadas destrezas, como serían la organización y el análisis de datos, y la creación de primeros y sencillos caminos. La mayoría de los grupos jugó animadamente, probó el funcionamiento de las piezas, creó caminos, los modificó, e incluso se adelantaron a algunas de las tareas de la sesión 2.

Respecto a la sesión 2, desde la observación del equipo de investigación y el análisis de los vídeos, se confirmó que las actividades no habían sido del todo adecuadas para la mayoría de los grupos. Solo algunos de ellos llegaban a las soluciones con facilidad y el resto lo hacían con serias dificultades, que provocaban frustración y aburrimiento. Para concretar el análisis, tanto en las sesiones 2 como en la 3, se han seleccionado los resultados de cuatro grupos cualesquiera, incluyendo al menos uno que tuviera más dificultades y un grupo que realizara las actividades con facilidad (se denominan grupos A, B, C y D, ver Figuras 2 y 3). En las tablas de las Figuras 2 y 3, se presenta el análisis llevado a cabo. La primera fila de las tablas contiene la etiqueta de los elementos que incluyen (Grupos de trabajo, Destrezas, Tareas); la primera columna contiene las denominaciones de los distintos grupos (cada grupo tiene asociado un color aleatorio), estando en la primera posición el resultado de un grupo modelo hipotético; la columna de destrezas incluye, para cada grupo, las cuatro destrezas a desarrollar; el resto de columnas presentan cronológicamente la secuencia de aparición de las destrezas asociadas al PC por grupo y por tarea.

Como ejemplo de una lectura de la tabla de la Figura 2, en el grupo modelo y, en este caso, también en el grupo A, en la Tarea 2.1, el alumnado lo primero que hace es organizar los elementos del juego de los que dispone, tanto piezas como canicas (“Organizar y/o analizar datos”), después coloca las piezas y canicas en el tablero (“Crear algoritmo”) y prueba si la respuesta es correcta (“Testear y depurar”). Se añade una letra B dentro de un recuadro verde en la tabla cuando la tarea se ha completado correctamente y se añade una letra M dentro de un recuadro rojo cuando no. Los cuadraditos coloreados indican la sucesión de destrezas encontradas. En el caso del grupo B, organiza los datos copiando el enunciado en el tablero y directamente intenta generalizar verbalmente a partir de una de las tareas de la sesión 1, vuelve a organizar los datos y prueba, obteniendo una respuesta errónea (M en rojo). Crea un nuevo algoritmo, prueba y obtiene respuesta correcta (B en verde).

Se comprueba que, en algunos casos, las actividades no se entendían con claridad en las fichas entregadas. Por ejemplo, a pesar de que el grupo A hiciera el camino correcto en la Tarea 2.2, accionó la palanca equivocada, realizando un primer testeo incorrecto, por no tener claro el enunciado (Figura 2).

Figura 2. Destrezas desarrolladas de PC por grupo y tarea y destrezas esperadas durante la sesión 2

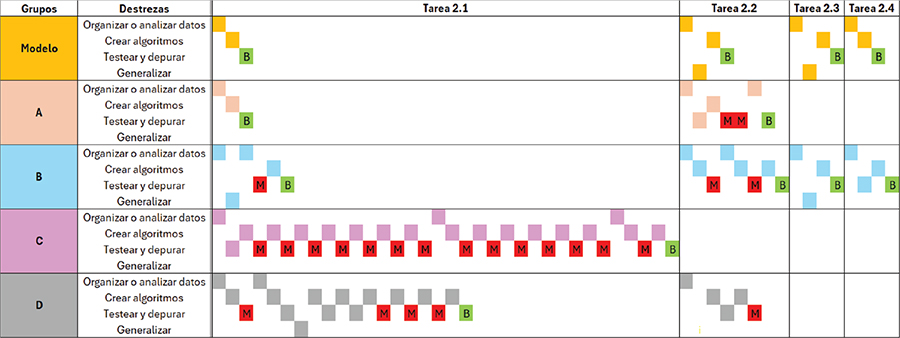
Por otro lado, se puede observar que los grupos C y D, en la Tarea 2.1, crean y testean continuamente, sin mucha reflexión sobre qué estaban haciendo. El grupo D optaba por probar a mitad del proceso para ver dónde caía la canica, sin predecir el posible camino. En esta tarea, mientras que el grupo D solo realizaba ensayo y error, hasta llegar a la solución, el grupo C tuvo que volver a leer el enunciado y hasta en dos ocasiones más reordenar las piezas y canicas para llegar a la solución. Tras la tercera organización y análisis de datos, el grupo C logró realizar la tarea correctamente.

En la sesión 3, la mayoría de los grupos finalizó casi todas las actividades (Figura 3). Por ejemplo, el grupo A consigue acabar todas las actividades, pero no llega a la solución en las Tareas 3.2.3 y 3.2.4; el grupo D resolvió todas de forma correcta; el grupo B solo dejó dos sin terminar, y durante los primeros minutos divagaba y se distraía con facilidad.

Figura 3. Destrezas desarrolladas de PC por grupo y tarea y destrezas esperadas durante la sesión 3

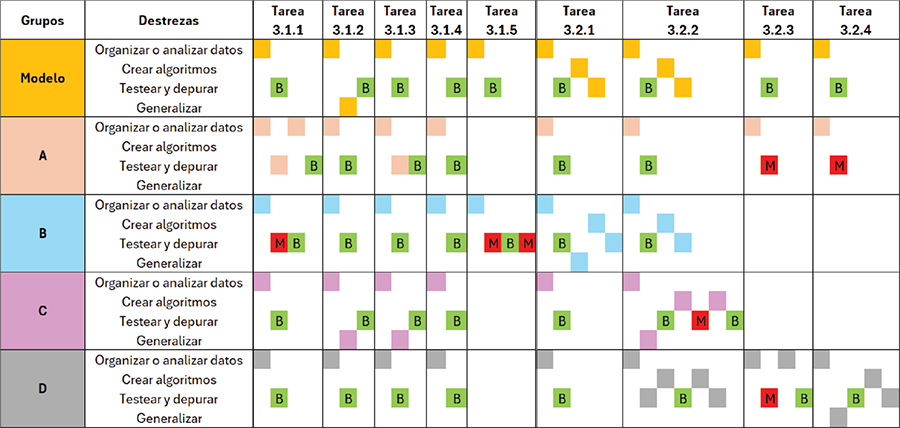
En esta sesión predominaban las tareas de reconocimiento de patrones y resultaron ser más accesibles para el alumnado que las de creación de caminos, ya que más grupos acababan las actividades (Figura 3). Es destacable como, mediante la gesticulación y la representación gráfica de los caminos, el alumnado era capaz de predecir sin necesidad de poner las piezas o probarlo realmente. Radford (2018) ya muestra la importancia de la gesticulación desde el punto de vista del pensamiento algebraico, ya que incita a la generalización y a la expresión de ideas más complejas, evitando el uso de números y símbolos. En muchas ocasiones el testeo correcto se realizaba solo en el papel, en otras se comprobaba luego en el tablero.

Comparando el análisis de las dos sesiones, se observa que grupos como el C y el D tuvieron dificultades con las tareas de la segunda sesión, mostrándose desmotivados y aburridos. Sin embargo, en la tercera sesión, cuando volvieron a obtener resultados satisfactorios, recuperaron el interés por las actividades.

Finalmente, en la sesión 4 se hizo una recopilación de actividades para afianzar conocimientos. El haber pasado previamente por la sesión 3, de predecir y completar caminos, facilitó entender y realizar las tareas.

Un aspecto común fue que el alumnado evitaba escribir en las fichas que se les proporcionaba para explicar e indicar qué habían hecho en las distintas tareas. Pasar de lo manipulativo a la representación simbólica, con dibujos en papel, fue todo un desafío que pocos realizaron.

4.2. Propuesta de mejora

Una vez se analizó el protocolo que se llevó a cabo en la intervención en el colegio, para las dos clases, se tomaron una serie de decisiones que han permitido obtener un nuevo protocolo de actuación mejorado, y mucho más realista y viable.

De partida, aunque la temática espacial de la UMASA fue motivadora para el alumnado, durante las distintas sesiones llamaba la atención, y se citó a Alan Turing y su papel en la II Guerra Mundial. Se decide que sería mucho más pertinente usar como referente a quien pone nombre al juego para contextualizar las actividades. Se incluyen en la nueva propuesta otros personajes como su compañera Joan Clarke. De esta forma, se nos permite entrar en aspectos mucho más formativos como el feminismo, la diversidad intelectual y afectivo-sexual, por las particularidades de estos personajes y sus historias (Sánchez Muñoz, 2018).

Por otro lado, pensando inicialmente en facilitar la manipulación de la documentación en el aula, las tareas fueron entregadas en unas fichas sueltas que resultaron poco atractivas. De hecho, el alumnado no solía marcar las soluciones en las hojas con naturalidad, aun requiriéndolo, dejando tareas sin respuesta. Para la nueva propuesta se realiza un cuaderno de trabajo más sugerente, contextualizado en la historia de Turing, en el que se incluyen todas las tareas de forma ordenada y secuenciada (Figura 4). Además, en cada hoja se añade la posibilidad de poder estampar un sello, tipo insignia, para motivar al alumnado. Este cuaderno sería entregado por grupo al inicio de la intervención, facilitando que puedan realizarse las tareas al ritmo particular de cada grupo.

Figura 4. Fichas en el protocolo anterior (izquierda) y nuevo cuaderno de trabajo (derecha)

Por otro lado, tras analizar las dificultades presentes en las sesiones, se evidenció que introducir tareas de creación de algoritmos en la segunda fue precipitado. En la nueva propuesta, tras la primera sesión con actividades de “cacharreo” y reconocimiento del juego, se incluyen tareas de predicción de resultados, de completar caminos (completar algoritmos), quitando piezas que no afectaban al resultado o detectando elementos del camino que causaban problemas en la solución esperada. Tras estas tareas, ya es pertinente incluir las tareas de creación de algoritmos. Y, finalmente, se proponen tareas de afianzar conocimientos.

En cada sesión, el alumnado debería tener claro cuáles son los objetivos de aprendizaje, qué se pretende con la intervención y qué finalidad tienen las tareas. Tras el análisis de la intervención, el equipo de investigación tomó conciencia de que no se hizo hincapié en estos objetivos en las sesiones. En la nueva propuesta, este momento debe estar adecuadamente planteado al inicio de las sesiones. De la misma forma, además al final de las sesiones, se debe incluir una reflexión de los aprendizajes adquiridos, siendo una forma imprescindible de tomar conciencia de qué ha ocurrido, por qué y cómo.

Otro de los problemas que han dificultado el análisis de los resultados han sido las grabaciones conjuntas de los grupos, que se materializaron en excesivo ruido y elementos distorsionantes. En la siguiente fase, la toma de datos se debe realizar en entornos de trabajo menos ruidosos, donde se puedan centrar las grabaciones en grupos pequeños.

Finalmente, se pueden mantener las cuatro sesiones de trabajo, así como el número de grupos y los cursos. Se considera que la temporalización es adecuada para tratar el tema con la narrativa de Alan Turing y la Segunda Guerra Mundial, mientras se desarrollan destrezas del pensamiento computacional.

5. Conclusiones

El objetivo de este trabajo era doble: analizar y mejorar la secuencia de tareas implementadas, evaluando su viabilidad en otros contextos educativos mediante el análisis de las respuestas del alumnado; y comprobar que el protocolo de investigación utilizado nos permitía recoger datos pertinentes que muestren el desarrollo de destrezas propias del PC en el alumnado de educación primaria. Tras el análisis realizado del protocolo inicial y la mejora propuesta para el mismo, podemos concluir que se ha conseguido el objetivo.

Se han detectado errores y dificultades presentes en la intervención en el aula del equipo de investigación, desde la forma de tomar la información en las clases con equipos de grabación para más de un grupo de trabajo, los documentos que se presentaron al alumnado para recoger los resultados de las tareas o la secuencia de las tareas, entre otros. Este proceso nos ha permitido mejorar el protocolo, detectando de forma muy concreta las fortalezas y las debilidades que contenía.

Respecto a las fortalezas, y una vez analizadas las destrezas propias del PC que se han desarrollado, se ha evidenciado que con este tipo de tareas el alumnado organiza y analiza datos, en este caso analiza las tareas planteadas y organiza las canicas y piezas; crea algoritmos, que aquí se traduce en crear caminos (a distintos ritmos y bajo distintos niveles de optimización); el alumnado es capaz de testear y depurar los algoritmos, mejorándolos o prediciendo resultados; y finalmente, aunque en menor medida, aplicaban generalizaciones a partir de soluciones y estrategias previas. Se observa, en la línea de Rodríguez et al. (2023), que las actividades desconectadas han aportado una serie de destrezas y conceptos abstractos correspondientes con el PC.

Una de las decisiones finales, que se ha tenido en cuenta para un siguiente ciclo de investigación, fue cambiar la secuencia de actividades, anteponiendo las de predecir resultados y las de completar caminos a las de creación de algoritmos. Durante la experiencia, se comprobó que las de creación eran de mayor complejidad. Por otro lado, el alumnado contaba con más tiempo para conocer las normas del juego (como evitar saltos de niveles, dar solo una vez a la palanca apropiada) y entender el funcionamiento de las piezas escogidas (Boswell y Boswell, 2021).

Esta propuesta didáctica permitiría desarrollar habilidades y destrezas que se han incluido en el currículo de primaria español dentro del sentido algebraico, en el área de matemáticas. Se presenta una secuencia de tareas desconectadas, que brinda al profesorado una opción viable y accesible para abordar el pensamiento computacional en el aula, sobre todo para quienes se sienten poco preparados para trabajar el PC en el aula (Santaengracia et al., 2023), más allá de experimentar con robots u ordenadores y programar con Scratch. Esta propuesta sigue implementándose y replicándose en nuevos contextos educativos, con mejoras continuas, y ha mostrado resultados altamente positivos que confirman la pertinencia y la efectividad del enfoque. Además, hay un fuerte potencial en el análisis del sentido socioafectivo, que es otra de las líneas futuras de este trabajo. Estos resultados continuarán siendo evaluados para consolidar la propuesta, aunque parte de su riqueza reside también en su flexibilidad.

6. Fuentes de financiación de la investigación

Esta investigación está enmarcada en el proyecto JAB1-34, código B1-2023_029 financiado por el Plan Propio de Investigación, Transferencia y Divulgación Científica de la Universidad de Málaga; dentro del grupo de investigación en el carácter funcional, formativo e instrumental de la didáctica de la matemática.

7. Referencias bibliográficas

Alsina, A. (2020). Itinerarios de enseñanza para el álgebra temprana. Revista Chilena de Educación Matemática, 12(1), 5-20. https://doi.org/10.46219/rechiem.v12i1.16

Arrifano Tadeu, P. J., & Brigas, C. (2022). El pensamiento computacional en educación infantil: un análisis a través del Computer Science Unplugged. Revista Interuniversitaria de Formación del Profesorado. Continuación de la Antigua Revista de Escuelas Normales, 97(36.2). https://doi.org/10.47553/rifop.v98i36.2.94881

Ayala-Altamirano, C., Arjona-Aranda, G., Moral-Sánchez, S. N., & Sánchez-Cruzado, C. (2024). Iniciación al pensamiento computacional a través de tareas desconectadas sobre patrones. En N. Adamuz-Povedano, E. Fernández-Ahumada, N. Climent, & C. Jiménez-Gestal (Eds.), Investigación en Educación Matemática XXVII (pp. 121-128). SEIEM.

Bocconi, S., Chioccariello, A., Kampylis, P., Dagienė, V., Wastiau, P., Engelhardt, K., Earp, J., Horvath, M. A., Jasutė, E., Malagoli, C., Masiulionytė-Dagienė, V., & Stupurienė, G. (2022). Reviewing Computational Thinking in Compulsory Education. Publications Office of the European Union. https://doi.org/10.2760/126955

Boswell, P., & Boswell, A. (2021). Turing Tumble: Libro de Problemas. Upper Story.

Brennan, K., & Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking [Comunicación]. American Educational Research Association meeting. Vancouver, Canada. https://scratched.gse.harvard.edu/ct/files/AERA2012.pdf

Cabra Páez, M. L., & Ramírez Gamboa, S. A. (2022). Desarrollo del pensamiento computacional y las competencias matemáticas en análisis y solución de problemas: una experiencia de aprendizaje con Scratch en la plataforma Moodle. Revista Educación, 46(1), 1-16. https://doi.org/10.15517/revedu.v46i1.44970

Confrey, J., & Lachance, A. (2000). Transformative teaching experiments through conjecture-driven research design. En A. E. Kelly, & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 231-265). Lawrence Erlbaum associates.

Curzon, P., McOwan, P., Plant, N., & Meagher, L. (2014). Introducing teachers to computational thinking using unplugged storytelling. En C. Schulte, M. E. Caspersen y H. Gal-Ezer (Coords.), WiPSCE’14 Proceedings of the 9th Workshop in Primary and Secondary Computing Education (pp. 89-92). Berlín, Alemania.

Denning, P. J., & Tedre, M. (2019). Computational thinking. The MIT Press (The Massachusetts Institute of Technology).

Furber, S. (2012). Shut down or restart? The way forward for computing in UK schools. The Royal Society.

Grover, S., & Pea, R. (2013). Computational Thinking in K-12: A Review of the State of the Field. Educational Researcher, 42, 1. https://doi.org/10.3102/0013189X12463051

Grover, S., & Pea, R. (2018). Computational Thinking: A Competency Whose Time Has Come. En S. Sentance, E. Barendsen, & C. Schulte (Eds.), Computer Science Education: Perspectives on Teaching and Learning in School (pp. 19-38). Bloomsbury Academic. https://doi.org/10.5040/9781350057142.ch-003

Iglesias, A., & Bordignon, F. (2021). Taxonomía de actividades desconectadas para el desarrollo de pensamiento computacional. Virtualidad, Educación y Ciencia, 22(12), 119-135.

Iyer, S. (2019). Teaching-Learning of Computational Thinking in K-12 Schools in India. En S. C. Kong, & H. Abelson (Eds.), Computational Thinking Education (pp. 362-382). Springer Open.

Jiménez, L. R., & Espinosa, C. I. (2019). Aprovechamiento del material manipulativo para fortalecer el pensamiento matemático en aula multigrado. Educación y Ciencia, 23, 513-529.

Kotsopoulos, D., Floyd, L., Khan, S., Namukasa, I. K., Somanath, S., Weber, J., & Yiu, C. (2017). A pedagogical framework for computational thinking. Digital Experiences in Mathematics Education, 3, 154-171. https://doi.org/10.1007/s40751-017-0031-2

Molina, M., Castro, E., Molina, J. L., & Castro, E. (2011). Un acercamiento a la investigación de diseño a través de los experimentos de enseñanza. Enseñanza de las Ciencias: Revista de Investigación y Experiencias Didácticas, 29(1), 75-88.

Orden de 30 de mayo de 2023, por la que se desarrolla el currículo correspondiente a la etapa de Educación Primaria en la Comunidad Autónoma de Andalucía. Boletín Oficial de la Junta de Andalucía, 104, de 2 de junio de 2023, pp. 9731/1-9731/208.

Papert, S. (1972). Teaching Children Thinking. Programmed Learning and Educational Technology, 9(5), 245-255. https://doi.org/10.1080/1355800720090503

Radford, L. (2018). The emergence of symbolic algebraic thinking in primary school. En C. Kieran (Ed.), Teaching and Learning Algebraic Thinking with 5- to 12-Year-Olds: The global evolution of an emerging field of research and practice (pp. 3-25). Springer.

Real Decreto 157/2022, de 1 de marzo, por el que se establecen la ordenación y las enseñanzas mínimas de la Educación Primaria. Boletín Oficial del Estado, 52, de 2 de marzo de 2022, pp. 24386-24504.

Rodríguez, J., Parra, G., Gili, G., Parra, S., Dolz, D., & Roumec, H. (2023). A Turing Machine at Secondary School. En P. Pesado (Ed.), Computer Science – CACIC 2022. Communications in Computer and Information Science, 1778(1), 295-306. Springer. https://doi.org/10.1007/978-3-031-34147-2_19

Sáez Vacas, F., & Delgado Kloos, C. (1979, 16-19 de octubre). Simulador de máquinas de Turing para fines didácticos [Comunicación]. 4.º Congreso Informática y Automática.

Sánchez Muñoz, J. M. (2018). Informe sobre la película “Descifrando Enigma”. Pensamiento Matemático, 8(2), 13.

Santaengracia, J. J., Palop, B., & Rodríguez-Muñiz, L. J. (2023). Percepciones del profesorado sobre pensamiento computacional. Estudio de una formación. En C. Jiménez-Gestal, Á. A. Magreñán, E. Badillo, E., & P. Ivars (Eds.), Investigación en Educación Matemática XXVI (pp. 491-498). SEIEM.

Sarmiento-Bolívar, M. I. (2019). Experiencias y estrategias educativas con TIC para el desarrollo del pensamiento computacional en Iberoamérica. Pensamiento Actual, 19(32), 12-27.

Selby, C., & Woollard, J. (2014). Refining an understanding of computational thinking. University of Southampton.

Seow, P., Looi, C. K., How, M. L., Wadhwa, B., & Wi, L. K. (2019). Educational Policy and Implementation of Computational Thinking and Programming: Case Study of Singapore. En S. C. Kong y H. Abelson (Eds.), Computational Thinking Education (pp. 345-361). Springer Open.

Sipser, M. (2013). The Church-Turing thesis. En M. Sipser (Ed.), Introduction to the theory of computation (pp. 137-163). Thomson Course Technology.

Sneider, C., Stephenson, C., Schafer, B., & Flick, L. (2014). Teacher’s Toolkit: Exploring the Science Framework and NGSS: Computational Thinking in the Science Classroom. Science Scope, 038(03), 10-15. https://doi.org/10.2505/4/ss14_038_03_10

Wing, J. M. (2006). Computational Thinking. Communications of the ACM, 49(3), 33-35. https://doi.org/10.1145/1118178.1118215

Wing, J. M. (2008). Computational thinking and thinking about computing. Philosophical Transactions of the Royal Society A, 366(1881), 3717-3725. https://doi.org/10.1098/rsta.2008.0118

Zapata-Ros, M. (2019). Pensamiento computacional desenchufado. Education in the Knowledge Society (EKS), 20, 1-29. https://doi.org/10.14201/eks2019_20_a18

_______________________________

(*) Autor de correspondencia / Corresponding author