CyberUnits Bricks: An Implementation Study of a Class Library for Simulating Nonlinear Biological Feedback Loops

• To provide a standardised toolkit for the rapid development of simulation software;

• To support simulation in time domain and frequency domain;

• To provide certain dynamic elements that are typical for living organisms;

• To achieve high performance of the created software solutions in terms of simulation speed, reliability and memory efficiency;

• To achieve the scalability of the generated models by supporting different temporal resolutions;

• To support the drawing of block diagrams to screen windows;

• To foster dimensional analysis and vertical translation between a molecular and an organism-wide level.

2. Methods

2.1. Mathematical Theory

The theory of linear feedback loops is well covered in the classical systems theory (DiStefano, 1990) and only briefly mentioned here (Fig. 1). Linear control systems follow the superposition principle, which is defined by additivity

Figure 1. Linear feedback loops of zeroth order (A) and first order (B). x: set point or reference input; y: controlled variable; v: rate of change of controlled variable; y_R: measured variable; z: load; e: error signal; u: controller output; G₁: controller gain; G₂: plant gain; α: gain of input signal in ASIA element; β: gain of signal deletion in ASIA element; ω: angular frequency

$$F\left(x_1+x_2\right)=F\left(x_1\right)+F\left(x_2\right)$$

and homogeneity

$$F\left(ax\right)=aF\left(x\right)\mathrm{.}$$

The concept of linear time-invariant (LTI) systems is dealt with by a mature theoretical structure today (Röhler, 1973; Varju, 1977; Glad and Ljung, 2000; Franklin et al., 2002). Methods have been developed for the analysis of the steady-state behaviour of linear feedback loops, of transitional effects in the time and frequency domain, and in the form of state space description. However, the usefulness of the LTI theory for living systems is rather limited.

In the organism, another nonlinear class of feedback control systems is common. It is marked by saturable properties of both stimulating and inhibiting elements. For a large class of biological phenomena, stimulating subsystems can be modelled with the Monod equation (applied as Michaelis-Menten kinetics, receptor theory and the Langmuir adsorption model) as

$$y(t)=\frac{Gx(t)}{D+Gx(t)},$$

where G denotes a maximum response (e.g., a secretory capacity or maximum enzyme activity under stimulated conditions) and D the magnitude of the input x that yields a half-maximum response.

Inhibiting subsystems are in most cases preferably represented as non-competitive inhibition with

$$y(t)=\frac{w(t)}{1+x(t)},$$

where w and x denote stimulating and inhibiting input signals, respectively. Combining these nonlinear elements delivers a form of feedback loop that is well-grounded in physiological foundations (Fig. 2).

Figure 2. Nonlinear MiMe-NoCoDI loop comprising saturation (Michaelis-Menten-like, MiMe) kinetics and non-competitive inhibition (NoCoDI) elements (Dietrich and Boehm, 2015)

Although the question of steady-state prognosis has been solved for an important class of nonlinear feedback loops (Dietrich and Boehm, 2015), no consistent mathematical methodology is available for the analysis of their temporal behaviour. This limitation can be overcome with computer simulations. To enable their rapid and efficient implementation, the following class library was developed.

2.2. Implementation of a Class Library

Expanding the theoretical issues of Section 2.1, we have developed CyberUnits Bricks, a universal class library that allows for the implementation of simulation software for a large range of linear and nonlinear feedback loops, including the kind of feedback control systems mentioned.

CyberUnits Bricks library is available along with documentation as open-source software with a BSD licence from https://cyberunits.sourceforge.net or https://doi.org/10.5281/zenodo.1304179. Supplementary material including source code for the benchmark programs is hosted by Zenodo, operated by CERN, and available via https://doi.org/10.5281/zenodo.8317319.

The class library comprises five units. The Bricks unit provides basic functionality that is sufficient for the modelling of all common variants of linear feedback control systems. The Lifeblocks unit includes additional classes for the simulation of heterogeneous nonlinear systems, as they are typical for living organisms. The SystemsDiagram unit supports the generation of block diagrams corresponding to the model structure. It was intentionally separated from the Bricks and Lifeblocks units so as not to thwart the development of non-visual programs (e.g., for command line interfaces or server-site software). Functionality for the analysis of time series with fast Fourier transform is included in the SignalAnalysis unit. The plots unit supports the graphical analysis of processing structures with Bode plots.

Three of the five units are object-oriented and provide classes for simulation and modelling (Fig. 3). Basic classes for all purposes are available in the Bricks unit, and more specialised functionality for the simulation of living organisms in the LifeBlocks unit. Visual classes for drawing blocks diagrams are collected in the SystemsDiagram unit. The units Plots and SignalAnalysis contain procedural code for Bode plots and fast Fourier transform of time series.

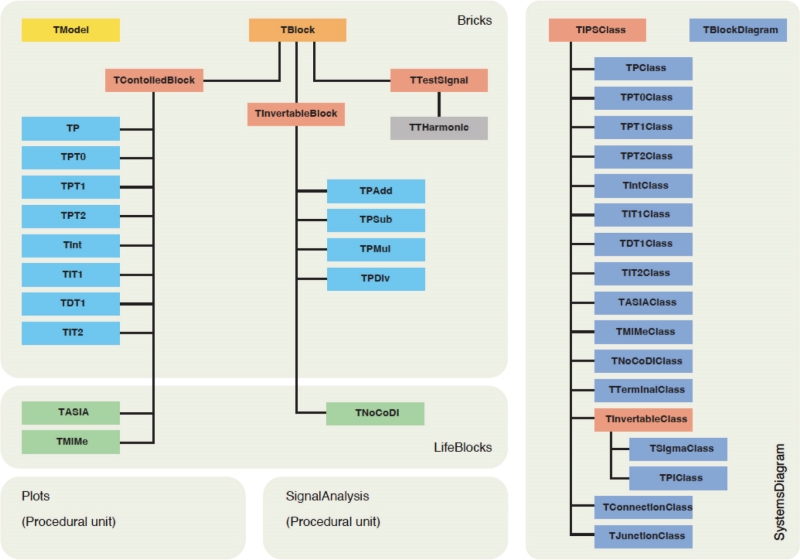
Figure 3. Class hierarchy of the CyberUnits Bricks library. See text and Table 1 for a more thorough explanation

A short summary of the available classes is provided in Table 1. Detailed information on the classes and units is provided in the documentation, which is available with the software, as described at the end of this article.

The class library was primarily implemented in Object Pascal. The reasons for this decision included the fact that Object Pascal is type-safe, available for a plethora of platforms, holds a well-readable source code, supports multiple modern programming paradigms and generates native and fast machine code with contemporary compilers (Kamburelis, 2023). It was written with the Lazarus IDE for the Free Pascal compiler (Free Pascal Team, 1991-2021; Lazarus Team, 1993-2023). All non-graphical units of the class library were extended with conditionals to support Embarcadero Delphi as well. The minimum requirements for the Object Pascal version are Free Pascal 3.2.2 and Lazarus 2.2.6 or newer, or Delphi 11.3 or newer, respectively. Simplified versions for Swift and C++ were written with Swift 5.8.1 or C++20 with GNU extensions, respectively, in Xcode 14.3.1 on macOS 13.4.1. Scripts for S and Python were text files that were interpreted and executed by the corresponding environments (R version 4.2.3 for macOS and Python 3.9.6 with Clang 14.0.3 on Darwin, respectively).

2.3. Speed Comparison

In addition to the implementation in Object Pascal, a representative subset of the library was also implemented in additional programming languages, including S, Python, C++ and Swift in order to compare the simulation speed among versions in different languages. S (in the R implementation) and Python are interpreted languages that enjoy high popularity in biomedical research and computational biology. C++ and Swift are compiled languages that were developed with the goal of being robust and type-safe and generating optimised and therefore fast machine code. Despite certain language-specific adaptations, the fundamental structure of the class library is identical in all language versions.

Two simulation programs, one for a first-order feedback loop (Fig. 1B) and one for a MiMe-NoCoDI loop (Fig. 2), were written in S, Python, Swift, C++ and Object Pascal. The programs were linked to the above-mentioned Bricks and Lifeblocks class libraries written in the respective languages. As with the libraries, language-specific adaptations were used, but the basic structure of the program flow was identical in all four implementations (Fig. 4).

Figure 4. Exemplary algorithms for basic simulation of a 0^th-order MiMe-NoCoDI loop (Fig. 2) and time measurements in Python, Swift and Object Pascal. See the online supplement for full source code in all evaluated programming languages

The simulations were implemented as command line interface (CLI) programs that were controlled via a Unix shell script. The shell script provided a loop mechanism that repeatedly invoked the simulation program with a systematic variation of the number of iteration steps (proportional to simulated time), ranging from 100 to 100,000 iterations with a step width of 50 iterations. Each step was repeated ten times so that benchmarks of 19,990 simulation runs were recorded for each programming language.

All simulation programs were executed on a MacBook Air Computer with Apple Silicon hardware (M2 processor, 8 cores, clock rate of up to 3.94 GHz, 24 GB of RAM) running macOS 13.4.1. During benchmarking, all non-essential services and background tasks were deactivated on the test machine. The software was either compiled for the AArch64 (A64) architecture or executed with an interpreter native for this instruction set.

2.4. Statistical Analysis

For a graphical representation of speed analysis, the mean values of all ten repetitions for each number of iterations were recorded and plotted. For statistical analysis, however, the data were evaluated in their original domain. Spearman correlations were used for the study of a potential relationship between iteration number and required time. For evaluating the correlations for different programming languages, models for pairs of two languages were compared under the assumption of independence with Fisher’s exact z-test and Zou’s confidence interval. The null hypothesis was that all correlations were equal. A p-value below an alpha-error threshold of 0.05 was regarded as significant.

To assess the relative contributions of the number of iterations and the programming language to the time of simulation a multivariable analysis was conducted, where a generalised linear model was fitted with an identity link function mapped to a gamma distribution.

All analyses were conducted with custom S scripts written for the statistical environment R (version 4.2.3 for macOS, R Core Team, 2023).

3. Results

3.1. Platform Availability

Thanks to the universal compatibility of modern Object Pascal compilers the class library is available for a large range of contemporary processor architectures (including x86-32, x86-64, PowerPC, ARM [AArch32 and AArch64]) and operating systems (e.g., MS Windows, macOS and several Linux variants). Major portions of the code have been implemented with compiler directives and conditionals to support both Free Pascal and Embarcadero Delphi. Visual classes have been written for the Lazarus Component Library (LCL) of the Lazarus IDE.

Test cases of the CyberUnits Bricks library and demo applications have been run on macOS, MS Windows and Raspbian Linux with Intel and ARM processors on 32-bit and 64-bit machines (Fig. 5).

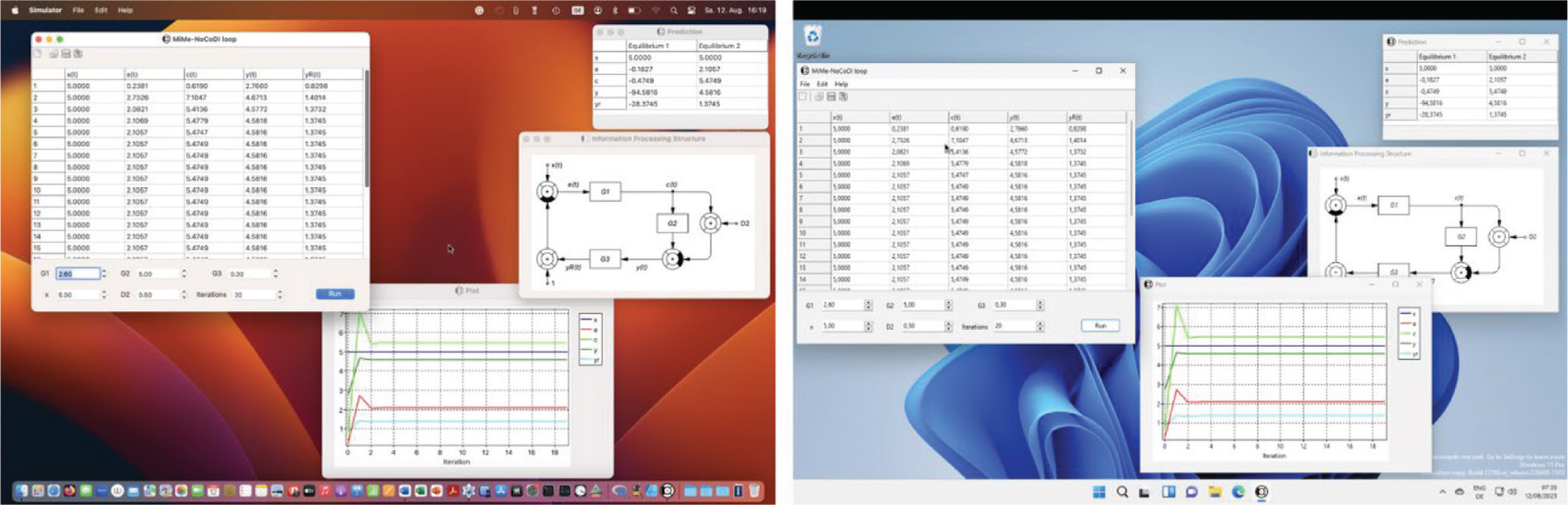
Figure 5. A simple simulator for a zeroth order MiMe-NoCoDI loop (see Fig. 2) written with CyberUnits Bricks on macOS 13.4 Ventura (Apple Silicon architecture, left) and Windows 11 (x86-64 architecture, right). The two implementations share the same source code, but run with native machine code and are optimized for the respective operating system as provided by the Lazarus Component Library (LCL) and the Free Pascal compiler. Shown are windows for time series in table form (top left of each screenshot) and graphical representation (bottom), the information processing structure as facilitated by the SystemsDiagram unit (right) and a steady-state prediction (top right, see Fig. 2 for a derivation of the equations). The simulated values rapidly approach the analytically predicted steady-state solution.

3.2. Simulation Speed

The speed of simulations was determined as the time needed for the completion of a simulation task (t_c) with different numbers of iterations (i). The number of iterations translates to simulated time (t_s) with

$$t_s=\delta i,$$

where δ represents the (uniform) step width of time-dependent simulation elements. Unlike t_s, t_c depends on the speed of the hardware and certain implementation details of the programming language and the operating system.

Irrespective of the number of iterations, Object Pascal yields the fastest and S the slowest programs. C++, Swift and Python are in between. The results for the two simulated feedback loops and the four tested programming languages are shown in Fig 6. For all languages, the required time significantly correlated with the number of iterations (p < 2.2e–16 for all relationships). Additionally, the correlations were different for all languages (p < 1e–4 and Zou’s 95% confidence interval not including 0).

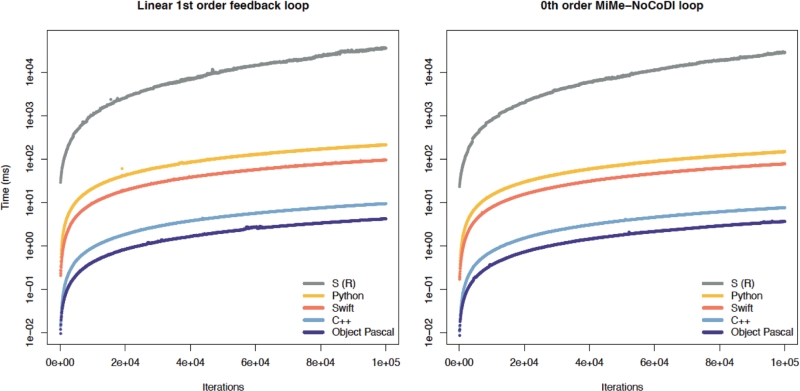
Figure 6. Simulation speed with implementations in different programming languages. Shown is the time needed to simulate a first-order linear feedback loop (A) and a zeroth-order MiMe-NoCoDI loop (B) dependent on the number of iterations (proportional to simulated time, abscissa) based on implementations of the simulation program and the CyberUnits Bricks library in S, Python, Swift, C++ and Object Pascal. The ordinate is logarithmically scaled and represents the mean of 10 replications of each number of iteration steps

In the models of multivariable regression analysis, the number of iterations and the programming languages are independent predictors of the time needed for simulation (Tables 2 and 3), with the exception of the pair of Swift and C++, which was not different. A variance inflation factor (VIF) of about one denotes virtually absent multicollinearity.

4. Discussion

With CyberUnits Bricks a versatile, cross-platform class library is available that supports modelling and simulation in life sciences. Its focus is on the simulation of feedback loops and similar motifs in systems biology.

We could provide evidence that the implementation in Object Pascal delivers a high performance of the generated modelling applications. Our results fit earlier observations which demonstrated that Pascal, the older non-object-oriented variant of the language, delivered the fastest implementation of several algorithms (QuickSort, Hailstone, sieve of Eratosthenes) compared to other programming languages, including C, C++, Go, Fortran, Rust and Python (Pereira et al., 2021). Additionally, Pascal was among the three Pareto optimal languages for the combination of time, memory usage and energy consumption of the hardware among a total of 27 programming languages (Pereira et al., 2021).

It is not the intention of the class library to replace existing products for modelling and simulation. Along these lines, it was not envisioned to offer an “out-of-the-box” solution by delivering directly usable simulation programs. The objective was, rather, to provide a versatile infrastructure for the creation of high-performance simulation solutions for complex systems in life sciences. Additionally, the availability of the class library helps to avoid reinventing the wheel by providing versatile and reusable building bricks of biological information processing structures for a range of platforms. Due to the implementation in a universal programming language, it can also lay the foundation for the making of stand-alone applications.

The class library has been successfully used in a simulation program for insulin-glucose homeostasis (Dietrich & Boehm, 2021; Dietrich et al., 2022) and is currently being employed to provide the basis for the next major version of a simulator of thyroid homeostasis for widespread use (SimThyr, Dietrich, 2017). When used with integrated development environments for rapid application development (RAD), such as Embarcadero Delphi or Lazarus, CyberUnits Bricks opens the way to the fast development of simulation programs. On this basis, an experienced developer can write a finished program for a simple feedback loop in less than 30 minutes.

On the other hand, the development of a simulation program requires some knowledge of programming. Therefore, CyberUnits Bricks is less suited for basic educational projects or the occasional use of simulation methods by unsophisticated persons without any background in software development. Its strengths are in versatility and performance.

5. Conclusion

CyberUnits Bricks is a universal class library that supports the development of computer simulations in life sciences with a focus on feedback loops and other control motifs in systems biology. Its main fork is developed in Object Pascal, thereby ensuring the high performance of the created software.

Future applications of the class library may target a large area of biomedical information processing structures and network motifs. This will require the support of additional signal transmission blocks, including Hill kinetics, and competitive and uncompetitive inhibition.

Currently, the Bricks library is being extended to fully support Embarcadero Delphi and RAD Studio as well. Thereby, developers and scientists will have more freedom of choice regarding the integrated development environment, and it will be possible to target a larger spectrum of platforms, ranging from smartphones to supercomputers.

Thanks to the high speed and the broad hardware support provided by the Object Pascal language, solutions built with CyberUnits Bricks may also find their way into devices of medical technology, e.g. insulin pumps with advanced hybrid closed-loop (AHCL) and automated insulin delivery (AID) algorithms. This step will considerably extend the scope of the class library from simulation to medical engineering, but it will also require the inclusion of extensive safety measures, as provided e.g. by the IEC 62304 standard and NASA’s Power of 10 rules (Holzmann, 2006).

6. Acknowledgements

This report is an extended version of a keynote lecture and a software presentation provided by the first author at the International Pascal Congress, held from July 3^rd to 7^th, 2023, in Salamanca.

7. References

Alon, U. (2007). Network motifs: theory and experimental approaches. Nature Reviews Genetics, 8, )450-61. https://doi.org/10.1038/nrg2102

Alon, U. (2020). An Introduction to Systems Biology. CRC Press.

Berberich, J., Dietrich, J. W., Hoermann, R., & Mueller, M. A. (2018). Mathematical Modeling of the Pituitary-Thyroid Feedback Loop: Role of a TSH-T-3-Shunt and Sensitivity Analysis. Front Endocrinol (Lausanne), 9. https://doi.org/10.3389/fendo.2018.00091

Cruz-Loya, M., Chu, B. B., Jonklaas, J., Schneider, D. F., & DiStefano, J., 3rd (2022). Optimized Replacement T4 and T4+T3 Dosing in Male and Female Hypothyroid Patients With Different BMIs Using a Personalized Mechanistic Model of Thyroid Hormone Regulation Dynamics. Frontiers in endocrinology, 13, 888429. https://doi.org/10.3389/fendo.2022.888429

Curcio, L., D'Orsi, L., Cibella, F., Wagnert-Avraham, L., Nachman, D., & De Gaetano, A. (2020). A Simple Cardiovascu-lar Model for the Study of Hemorrhagic Shock. Computational and mathematical methods in medicine, 2020, 7936895. https://doi.org/10.1155/2020/7936895

Dietrich, J. W. (2002). Der Hypophysen-Schilddrüsen-Regelkreis. Entwicklung und klinische Anwendung eines nichtlinearen Modells (Vol. 2). Logos-Verlag.

Dietrich, J. W. (2017). SimThyr. Report No. RRID:SCR_014351, (Zenodo, 2017).

Dietrich, J. W., & Boehm, B. O. (2006). Equilibrium behaviour of feedback-coupled physiological saturation kinetics. In Trappl R. (ed.), Cybernetics and Systems 2006 (Vol. 1, pp. 269-274). Austrian Society for Cybernetic Studies.

Dietrich, J. W. & Boehm, B. O. (2015). Die MiMe-NoCoDI-Plattform: Ein Ansatz für die Modellierung biologischer Regelkreise. German Med. Sci. DocAbstr. 284. https://doi.org/10.3205/15gmds058

Dietrich, J. W. & Boehm, B. O. (2021). SimulaBeta. Report No. RRID: SCR_021900, (Zenodo, 2021).

Dietrich, J. W., Dasgupta, R., Anoop, S., Jebasingh, F., Kurian, M. E., Inbakumari, M., Boehm, B. O., & Thomas, N. (2022). SPINA Carb: a simple mathematical model supporting fast in-vivo estimation of insulin sensitivity and be-ta cell function. Scientific reports, 12(1), 17659. https://doi.org/10.1038/s41598-022-22531-3

Dietrich, J. W., Landgrafe-Mende, G., Wiora, E., Chatzitomaris, A., Klein, H. H., Midgley, J. E., & Hoermann, R. (2016). Calculated Parameters of Thyroid Homeostasis: Emerging Tools for Differential Diagnosis and Clinical Research. Frontiers in endocrinology, 7, 57. https://doi.org/10.3389/fendo.2016.00057

Dietrich, J. W., Mitzdorf, U., Weitkunat, R., & Pickardt, C. R. (1997). The pituitary-thyroid feedback control: stability and oscillations in a new nonlinear model. Journal of Endocrinological Investigation, 20 (Suppl. to no. 5), 100.

Dietrich, J. W., Tesche A., Pickard C. R. and Mitzdorf U. (2004). Thyrotropic feedback control: Evidence for an addition-al ultrashort feedback loop from fractal analysis. Cybernetics and Systems, 35(4), 315-331. https://doi.org/10.1080/01969720490443354

DiStefano, J. (1990). Schaum’s Outline of Feedback and Control System. McGraw-Hill.

Franklin, G. F., Powell, J. D., Emami-Naeini, A. (2002). Feedback Control of Dynamic Systems. Prentice Hall.

Free Pascal Team. (1993-2023). Free Pascal: A 32-, 64- and 16-bit professional Pascal compiler. Report No. RRID: SCR_014360, (Fair-fax, VA, 1993-2023).

Glad, T., Ljung, L. (2000). Control Theory. Taylor & Francis.

Han, S. X., Eisenberg, M., Larsen, P. R., & DiStefano, J., 3rd (2016). THYROSIM App for Education and Research Pre-dicts Potential Health Risks of Over-the-Counter Thyroid Supplements. Thyroid: official journal of the American Thyroid Association, 26(4), 489-498. https://doi.org/10.1089/thy.2015.0373

Head, R. J., Lumbers, E. R., Jarrott, B., Tretter, F., Smith, G., Pringle, K. G., Islam, S., & Martin, J. H. (2022). Systems analysis shows that thermodynamic physiological and pharmacological fundamentals drive COVID-19 and re-sponse to treatment. Pharmacology research & perspectives, 10(1), e00922. https://doi.org/10.1002/prp2.922

Hoermann, R., Midgley, J. E. M., Larisch, R., & Dietrich, J. W. (2013). Is pituitary TSH an adequate measure of thyroid hormone-controlled homoeostasis during thyroxine treatment? European Journal of Endocrinology, 168(2), 271-280. https://doi.org/10.1530/EJE-12-0819

Hoermann, R., Midgley, J. E., Larisch, R., & Dietrich, J. W. (2015). Homeostatic Control of the Thyroid-Pituitary Axis: Perspectives for Diagnosis and Treatment. Front Endocrinol (Lausanne), 6, 177. https://doi.org/10.3389/fendo.2015.00177

Hoermann, R., Pekker, M. J., Midgley, J. E. M., Larisch, R., & Dietrich, J. W. (2022). Principles of Endocrine Regulation: Reconciling Tensions Between Robustness in Performance and Adaptation to Change. Frontiers in endocrinology, 13, 825107. https://doi.org/10.3389/fendo.2022.825107

Holzmann, G. (2006). The Power of 10: Rules for Developing Safety-Critical Code. IEEE Computer. 39(6), 95-9. https://doi.org/10.1109%2FMC.2006.212

Kamburelis, M. (2023). Why use Pascal? https://castle-engine.io/why_pascal

Kolar-Anić, L., Čupić, Ž., Maćešić, S., Ivanović-Šašić, A., & Dietrich, J. W. (2023). Modelling of the thyroid hormone synthesis as a part of nonlinear reaction mechanism with feedback. Computers in biology and medicine, 160, 106980. https://doi.org/10.1016/j.compbiomed.2023.106980

Lazarus Team. (1993-2001). Lazarus: The professional Free Pascal RAD IDE. Report No. RRID: SCR_014362, (Fairfax, VA, 1993-2021).

McEwen B. S. (1998). Stress, adaptation, and disease. Allostasis and allostatic load. Annals of the New York Academy of Sciences, 840, 33-44. https://doi.org/10.1111/j.1749-6632.1998.tb09546.x

McEwen, B. S., & Stellar, E. (1993). Stress and the individual. Mechanisms leading to disease. Archives of internal medicine, 153(18), 2093-2101. https://doi.org/10.1001/archinte.1993.00410180039004

Midgley, J. E. M., Hoermann, R., Larisch, R., & Dietrich, J. W. (2013). Physiological states and functional relation be-tween thyrotropin and free thyroxine in thyroid health and disease: in vivo and in silico data suggest a hierarchical model. J Clin Pathol, 66(4), 335-342. https://doi.org/10.1136/jclinpath-2012-201213

Neuber, H. (1989). Simulation von Regelkreisen auf Personal Computern in Pascal und Fortran 77. IWT.

Pereira, R., Couto, M., Ribeiro, F., Rua, R., Cunha, J., Fernandes, J. P., & Saraiva, J. (2021). Ranking programming lan-guages by energy efficiency. Science of Computer Programming, 205, 102609. https://doi.org/10.1016/j.scico.2021.102609

Pompa, M., Panunzi, S., Borri, A., & De Gaetano, A. (2021). A comparison among three maximal mathematical models of the glucose-insulin system. PloS one, 16(9), e0257789. https://doi.org/10.1371/journal.pone.0257789

R Core Team. (2023). R: A Language and Environment for Statistical Computing. Report No. RRID:SCR_001905, (R Foundation for Statistical Computing, Vienna, Austria, 2018).

Röhler, R. (1973). Biologische Kybernetik - Regelungsvorgänge in Organismen. Vieweg+Teubner Verlag. https://doi.org/10.1007/978-3-322-94729-1

Schulkin, J., & Sterling, P. (2019). Allostasis: A Brain-Centered, Predictive Mode of Physiological Regulation. Trends in neurosciences, 42(10), 740-752. https://doi.org/10.1016/j.tins.2019.07.010

Tretter F. (2018). From mind to molecules and back to mind-Metatheoretical limits and options for systems neuropsychiatry. Chaos, 28(10), 106325. https://doi.org/10.1063/1.5040174

Tretter, F., Wolkenhauer, O., Meyer-Hermann, M., Dietrich, J. W., Green, S., Marcum, J., & Weckwerth, W. (2021). The Quest for System-Theoretical Medicine in the COVID-19 Era. Frontiers in medicine, 8, 640974. https://doi.org/10.3389/fmed.2021.640974

Tretter, F., Peters, E. M. J., Sturmberg, J., Bennett, J., Voit, E., Dietrich, J. W., Smith, G., Weckwerth, W., Grossman, Z., Wolkenhauer, O., & Marcum, J. A. (2023). Perspectives of (/memorandum for) systems thinking on COVID-19 pandemic and pathology. Journal of evaluation in clinical practice, 29(3), 415-429. https://doi.org/10.1111/jep.13772

Varjú, D. (1977). Systemtheorie für Biologen und Mediziner. Springer-Verlag,

Wolff, T. M., Veil, C., Dietrich, J. W., & Muller, M. A. (2022). Mathematical modeling and simulation of thyroid homeo-stasis: Implications for the Allan-Herndon-Dudley syndrome. Front Endocrinol (Lausanne), 13, 882788. https://doi.org/10.3389/fendo.2022.882788