ADCAIJ: Advances in Distributed Computing and Artificial Intelligence Journal
Regular Issue, Vol. 14 (2025), e31698
eISSN: 2255-2863
DOI: https://doi.org/10.14201/adcaij.31698
Matrix Hashing with Random Probing in 1D Array
Rajeev Ranjan Kumar Tripathia, Pradeep Kumar Singhb, and Sarv Pal Singhc
a Department of Computer Science and Engineering, Madan Mohan Malaviya University of Technology, Gorakhpur, Uttar Pradesh, India, 273008
b Department of Computer Science and Engineering, Madan Mohan Malaviya University of Technology, Gorakhpur, Uttar Pradesh, India, 273008
c Department of ITCA, Madan Mohan Malaviya University of Technology, Gorakhpur, Uttar Pradesh, India, 273008
rajeevranjankumartripathi@gmail.com, topksingh@gmail.com, singhsarvpal@gmail.com
ABSTRACT
The current computing era enables the generation of vast amounts of data, which must be processed to extract valuable insights. This processing often requires multiple query operations, where hashing plays a crucial role in accelerating query response times. Among hashing techniques, Cuckoo Hashing has demonstrated greater efficiency than conventional methods, offering simplicity and ease of integration into various real-world applications. However, Cuckoo Hashing also has limitations, including data collisions, data loss due to collisions, and the potential for endless loops that lead to high insertion latency and frequent rehashing. To address these challenges, this work introduces a modified Matrix hashing technique. The core concept of the proposed scheme is to utilize both a 2D array and an additional 1D array with random probing to create a more robust technique that competes effectively with Cuckoo Hashing. This study also introduces degree of dexterity as a new performance metric, in addition to the traditional load factor. Furthermore, the Even-Odd hash function is proposed to ensure a more balanced load distribution. Through rigorous experimental analysis in a single-threaded environment, this modified Matrix hashing with random probing in the 1D array is shown to effectively resolve key issues associated with Cuckoo Hashing, such as excessive data migration, inefficient memory usage, and high insertion latency.
KEYWORDS
Cuckoo Hashing; degree of dexterity; load factor; Even-Odd hash function
1. Introduction
The continuous and rapid advancements in mobile computing, the Internet of Things (IoT), cloud computing, distributed systems, and social media have drawn considerable attention from both the public and industries. Consequently, there has been an immense and unprecedented surge in data generation, encompassing various forms such as text, audio, video, graphics, images, and animation. Among these, multimedia data requires significantly more storage than other types. Substantial progress has been made in data storage technologies, with data centres serving as prime examples of these achievements. Common operations on stored data include insertion, deletion, updating, and searching, and data itself can be classified as either structured or unstructured. A classic challenge in computer science is the efficient storage of information to allow quick retrieval upon request (Awad et al., 2023). This kind of search is commonly employed in data dictionaries, compiler-maintained symbol tables, and the database industry. Information is stored as records in computer memory, which can be either fixed-length or variable-length. Each record is identified by a unique key, which may be generated from the information in the record or explicitly assigned by an administrator. Notably, the key’s size does not affect the search process. A search algorithm takes a key, k, as input and returns the associated record. In computer memory, data structures can be represented through either contiguous or non-contiguous memory allocation. Linear search techniques, which traverse data sequentially, do not require sorted input. However, for large datasets, linear search is time-consuming, with a time complexity proportional to the data size. In contrast, binary search significantly outperforms linear search by narrowing the search space with each unsuccessful comparison, achieving a time complexity of (log2n), where n is the number of keys. The effectiveness of binary search inspired the development of data structures using non-contiguous memory allocation that support binary search, leading to the creation of the Binary Search Tree (BST). Although BSTs perform well on average, their efficiency degrades to that of linear search when the input is already sorted. To counter this, balanced tree variants, such as AVL and Red-Black trees, were introduced, which maintain height balance and enhance search efficiency. In search trees, search time correlates with the tree’s height, meaning that as the dataset grows, so does the search time (Shi and Qian, 2020). This spurred further research into techniques that would make search time independent of dataset size.
Hashing emerged as a solution by assigning data to addresses based on a hash function: h = H (k), where H is the hash function, h is the generated address (also called the hash code or hash value), and k is the key to be stored. The key and its corresponding hash value can be represented as an ordered pair (h, k). Ideally, hashing enables searching in constant time, O (1) (Pontarelli et al., 2018). However, due to the variability of data and hash functions, achieving unique (h, k) pairs is not always feasible, leading to a problem known as hash collision. Collisions occur when two different keys, K1 and K2, produce the same hash code, resulting in (h, K1) = (h, K2). Such keys are called synonyms. Hans Peter Luhn was the first to demonstrate the concept of hashing (Stevens, 2018).
2. Literature Survey
Hashing methods can broadly be classified into two categories: Data-Oriented Hashing and Security-Oriented Hashing. In security-oriented hashing, the primary goal is to ensure data integrity by using hash functions. In contrast, data-oriented hashing aims to retrieve information from a file or database in constant time (Balasundaram and Sudha, 2021). Data-oriented hashing is further divided into two main types: Data-Independent Hashing and Data-Dependent Hashing (Cai, 2021).
Data-Independent Hashing does not rely on labeled data and does not require any training. Based on the underlying projection methods, it can be further divided into four types: Random Hashing, Locality Sensitive Hashing (LSH), Learned Hashing, and Structured Projection. Locality Sensitive Hashing (LSH) and Learned Hashing, both subtypes of data-independent hashing, can adapt to data distributions to enhance hashing performance. Data-Dependent Hashing, on the other hand, is highly sensitive to the characteristics of the underlying data and thus requires training. Data-dependent hash functions are categorized into three subtypes based on the availability of labeled information in the training dataset as Unsupervised Hashing, Semi-Supervised Hashing, and Supervised Hashing, which relies entirely on labeled data (Liang and Wang, 2017). Each of these methods offers different levels of adaptability and precision, depending on the nature and availability of data used during the hashing process (Bai et al., 2014). Classifications of hashing techniques are shown in Figure 1 (Chi and Zhu, 2017), (Fang et al., 2017), (Suruliandi, 2024), (García-Peñalvo, 2024).
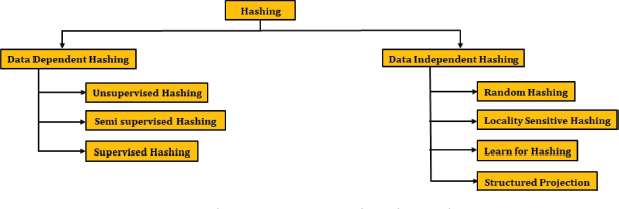
Figure 1. Classification of Data Independent Hashing
The key properties expected from a hash function are outlined in Table 1.
Table 1. Properties of Hash Functions
Properties |
Details |
Deterministic |
A hash function must consistently generate the same hash value for a given input, ensuring reliable data storage and retrieval. |
Efficient Computation |
Hash functions should be computationally efficient, allowing for quick computation of hash values even with large inputs. This efficiency is essential for optimal performance in real-time applications. |
Uniform Key Distribution |
An effective hash function distributes input values uniformly across the hash table, minimizing collisions. This uniform distribution ensures that each slot in the hash table has an equal likelihood of being used. |
Minimization of Collisions |
Although it is impossible to completely avoid collisions where different inputs yield the same hash value, a well-designed hash function minimizes their frequency. When collisions do occur, methods such as chaining and open addressing are used to manage them effectively. |
Statelessness |
Hash functions are stateless, meaning they do not retain information between executions. Each hash computation operates independently of previous or future calculations, ensuring predictability and consistency. |
Idempotency |
When a hash function is applied to an already hashed output, the result should remain unchanged. This property is essential for specific recursive data structures and applications. |
Simplicity |
A good hash function should be straightforward to implement and understand, facilitating its integration into a wide range of applications. |
Avalanche Effect |
The avalanche effect ensures that even slight changes to the input data result in significant alterations to the output. |
2.1. Popular Hash Functions
The division method is particularly simple due to its ease of implementation. In this method, the remainder division is performed between the key, k, and a chosen value M. When M is selected wisely, this method can yield better results compared to other hash functions. The value of M should be a prime number close to the size of the hash table. There are two variants of this method: (k mod M) and (k mod M)+1. The appropriate version is chosen based on the starting address of the table. The prime number M helps distribute the keys uniformly across the available addresses (Maurer and Lewis, 1975).
In the mid-square method, the key k is squared, and an equal number of digits are discarded from both the left and right sides of the result. The remaining middle digits are then used as the address. The number of digits discarded from each side depends on the number of digits required for the table’s addresses.
The folding method also depends on the number of digits, r, available in the table’s addresses. In this method, the key is divided into groups of r digits, starting from the left. If necessary, padding is added to the final group. The groups are then summed, with any carry in the most significant digit discarded.
Universal family of hashing, H, is a set of hash functions, Hi ∈Z that map given universe, U, of keys to the addresses in the range {1, 2, 3, ... m − 1}. For any chosen hash function, Hi ∈ H on random basis and any pair of keys, x and y, ∀ (x, y) ∈ U, probability of collision, Pr (H1 (x) = H1 (y)), is (1/m) (Carter and Wegman, 1979).
2.2. Collision Resolution Techniques
Any application that utilizes a hash table must select both a hash function and a collision resolution technique. Collision resolution techniques can be categorized into three main types: open addressing, chaining, and coalesced hashing. In open addressing, if the hash code of a key is already occupied by another key, the key is stored in a different available location. Open addressing primarily uses four methods to resolve collisions: linear probing, quadratic probing, random probing (uniform hashing), and double hashing, as illustrated in Figure 2 (Debnath et al., 2010).
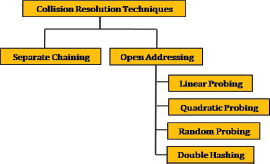
Figure 2. Collision Resolution Techniques in Hashing
In linear probing, the algorithm searches for an empty slot sequentially from the point of collision, moving toward both ends of the table. If an empty slot is found, the key is placed there; otherwise, the key is discarded. Quadratic probing searches for an empty slot in a quadratic manner, starting from the point of collision and progressing in the sequence H(k)+12, H(k)+22, H(k)+32 and so on. When the table size is a prime number, this method accesses half of the table’s locations on average (Guibas, 1978).
In random probing, the search for empty slots is conducted randomly. Random probing is often used as a theoretical model for double hashing and similar methods that aim to minimize clustering (Fan et al., 2013), (Jiménez, 2018). In the double hashing scheme, a second hash function, H’, is employed to resolve collisions. If a collision occurs for key k, the algorithm searches for an empty slot following the sequence H(k)+H’(k), H(k)+2H’(k), H(k)+3H’(k), and so on. The second hash function, H’, must generate a smaller hash value than the size of the table, and this is why H’ must be carefully chosen (Wu et al., 2022).
Insertion, deletion, and key searching require additional probes when open addressing is used. The need for extra probes increases the average search length (Wu et al., 2021). Collision resolution techniques are depicted in the Figure 2.
In separate chaining (chaining), there is an array of buckets (LIST), where each bucket holds the starting address of a linked list. The hash code, H(k), is computed using the hash function H, and the key is inserted into the linked list at LIST[H(k)]. In chaining, the load factor (λ) is the ratio of the number of keys stored to the size of the list. The load factor may exceed 1.0 in chaining. Each bucket in chaining represents a cluster of records. The operations of insertion, deletion, and searching are carried out in the same manner as they would be in a linked list (Larson, 1983), (Vitter, 1983).
2.3. Cuckoo Hashing
Cuckoo Hashing is a randomized, nature-inspired hashing technique that utilizes two tables, denoted as T1 and T2, which can either be of the same size or different sizes, along with two hash functions, H1 and H2 (Pagh, 2001), (Pagh and Rodler, 2004), (Ferdman et al., 2011). When the tables are of equal size, the method is referred to as Symmetric Cuckoo Hashing, while if the tables differ in size, it is called Asymmetric Cuckoo Hashing. These hash functions distribute the key universe, U, across both T1 and T2. A key k is stored either at T1[H1(k)] or T2[H2(k)], requiring at most two lookup operations in the worst case.
In its traditional form, Cuckoo Hashing executes these lookup operations sequentially. However, researchers have introduced the concept of Parallel Cuckoo Hashing, which allows for concurrent access. The two main variants of Cuckoo Hashing are categorized based on the way the hash tables are accessed: Parallel Cuckoo Hashing and Sequential Cuckoo Hashing (also known simply as Cuckoo Hashing). The latter is further divided into Symmetric Cuckoo Hashing and Asymmetric Cuckoo Hashing, based on whether the tables are of equal or differing sizes (Patel and Kasat, 2017), (Skarlatos et al., 2020).
The designers of Cuckoo Hashing proposed a relationship between the size of the tables (n) and the number of keys (R) as n ≥(1 +ϵ)R where ϵ is a constant and ϵ≥0 in the case of Symmetric Cuckoo Hashing. In Asymmetric Cuckoo Hashing, one table is twice the size of the other, resulting in greater memory usage compared to Symmetric Cuckoo Hashing. When a collision occurs, Cuckoo Hashing resolves it by displacing existing keys to make space for new ones. This «kicking out» process continues until a threshold, referred to as «MaxLoop», is reached, after which a rehash operation is triggered. The hash functions H1 and H2 are chosen from a Universal Family of Hash Functions with complexity orders of O(1) and O(logn), respectively. However, Cuckoo Hashing presents certain challenges, including a) inefficient memory usage, b) data migration, and c) higher insertion latency (Sun et al., 2016). The conceptual view of Symmetric Cuckoo Hashing and Asymmetric Cuckoo Hashing are shown in Figures 3 and 4 (Minaud and Papamanthou, 2023).
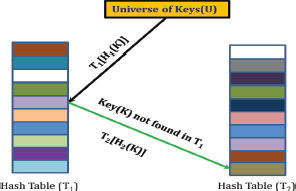
Figure 3. Conceptual View of Symmetric Cuckoo Hashing
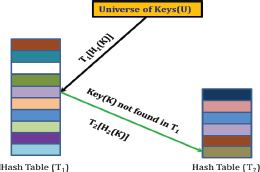
Figure 4. Conceptual View of Symmetric Cuckoo Hashing
2.4. Combinatorial Hashing
Ronald L. Rivest has classified information retrieval queries into six types: exact-match queries, partial-match queries, single-key queries, range queries, best-match queries with restricted distance, and Boolean queries. Partial-match queries utilize the symbols 0, 1, and *, where * represents an unspecified value. Such queries are useful in applications like a crossword puzzle dictionary; for example, the query «A**I*E» might return words such as «ADVICE», «ACTIVE», «ARRIVE», and «ADVISE». Rivest suggests applying a hash function to each letter in a word; for instance, «ADVICE» would be hashed as H(A)||H(D)||H(V)||H(I)||H(C)||H(E). If the hash function produces a 2-bit code for each letter, the resulting hash table would have 2^12 entries. For a query like «A**I*E», rather than searching all 212 entries, one would only need to search 26 locations, significantly reducing search complexity. Figure 5 illustrates the concept of combinatorial hashing (Kurpicz, 2023).
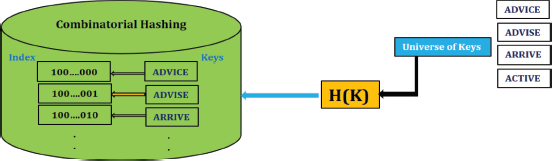
Figure 5. Collision Resolution Techniques in Hashing
3. Contribution
In addition to the load factor, denoted as λ, the authors introduce a new parameter called the Degree of Dexterity (η) to evaluate the efficiency of a hash function. They also propose an innovative method for selecting a prime number, which is used in the division method to achieve an even load distribution. In this context, the division method (which incorporates the prime number) is referred to as the Even-Odd Hash Function.
Contribution 1: The performance of hash functions cannot be assessed solely by λ and search time. In previous research, insertion latency was considered but was not used as a metric for evaluating hashing efficiency. Information retrieval from a hash table occurs only after key insertion is complete, and insertion latency reflects the total time required to populate the hash table. This paper is the first to introduce the Degree of Dexterity (η) as a new performance indicator in hashing.
Contribution 2: For a given universe of keys, denoted by U, a key K with a maximum width W is selected. The prime number P should be slightly larger than and close to 2W. Given |U|=n, a matrix of order P×KPB is used as the primary hash table to store the keys. In this work, this primary hash table is called the Matrix Hash Table. Thus, the matrix hash table logically consists of P tables, with each table having a size of KPB. As each digit in K may be even or odd due to the selection of P based on 2W, the authors refer to this scheme as the Even-Odd Hash Function.
The factor ϕ serves as an equalization parameter, impacting the effective memory utilization of the Matrix hash table.
Contribution 3: This work thoroughly examines the performance of Cuckoo Hashing. Experimental results indicate that Symmetric Cuckoo Hashing can result in the loss of a single key, as it employs hash functions from the family of universal hash functions. For the same set of keys, Symmetric Cuckoo Hashing and Asymmetric Cuckoo Hashing exhibit varied performance in terms of search cost and insertion latency.
4. Problem Formulation and Motivation of Current Work
In the field of hashing, load factor, insertion latency, and average search length are key performance indicators. The load factor is defined as the ratio of the number of stored keys to the total number of available locations in the hash table, providing an average value of keys per location. For an ideal hash function, both the load factor and the average search length are 1.In this study, the authors aim to develop a hash function with a predictable load factor, referred to as KPB. Drawing inspiration from combinatorial hashing, they introduce a new method called the Even-Odd Hash Function, which is based on the division method. While universal hash functions are generally more computationally intensive than division-based methods, the Even-Odd Hash Function offers a more efficient alternative.
The primary goal of this work is to evaluate the performance of the Even-Odd Hash Function in comparison to Universal Hash Functions on a large dataset. The Even-Odd Hash Function prototype is specifically benchmarked against Cuckoo Hashing to assess its efficiency and effectiveness.
5. Current Work: Even-Odd Hash Function and Matrix Hashing with Random Probing in 1D Array
5.1. Even-Odd Hash Function
Even-Odd hash function based on Combinatorial Hashing. The hash code for each digit is considered as 2. The longest key from the U is chosen and its width W is considered to generate a prime number, Prime(2W). Prime(2W) is used in division method to generate the hash code. Authors refer to this hash function as Even-Odd hash function because an individual digit in a key may be either even or odd. If individual digits are examined in odd-even tests, it leads to a high computational cost with an increase in the width of the key. Authors have generalized this and performed the exponentiation operation of 2 with W.
5.2. Matrix Hashing with Random Probing in 1D Array
The proposed scheme employs two hash tables: a Matrix hash table (a 2D array) and a Backup table (a 1D array). The Even-Odd hash function utilizes the division method, selecting a prime number (denoted as P) as the divisor, where P>2W, and W is the maximum width of a key from the key set U. Let |U|=n. The average Key per Bucket (KPB) is approximately , and the Even-Odd hash function distributes keys according to this KPB value. The Matrix hash table is structured as a collection of 1D arrays. To enhance the performance of the Even-Odd hash function, the parameter ϕ has been introduced. Although ϕ improves performance, it directly impacts the size of the Matrix hash table; hence, choosing an optimal value for ϕ is essential for efficient memory utilization. The Backup table size is set to f×P×KPB, where f is a constant, set to 0.49 in this work. The constants ϕ and f are key parameters influencing the overall space complexity of the proposed scheme. In this study, the equalization factor ϕ is set to 1.5.
The scheme uses the division method to determine the number of columns (C), while row number (R) is determined by the Even-Odd hash function. Each key (k) is stored in Matrix[R][C] without collisions. In the case of a collision, however, keys are moved to the Backup table, where quadratic and random probing techniques resolve the conflicts. Three quadratic probing methods are employed: conventional quadratic probing, quadratic probing with prime numbers, and Fibonacci numbers. For random probing, finite sets of prime and Fibonacci numbers are used.
To locate empty positions, a left-to-right search approach is applied in the Backup table, while the finite sets of Fibonacci and prime numbers help to reduce the average search length, resulting in enhanced performance.
i.Create and Initialize MatrixHashTable;
ii.Create and Initialize BackupTable;
Procedure: insert (Key K);
1.R = computeRow(K);
2.C = computeCol(K);
3.if MatrixHashTable[R][C] is empty then
a.MatrixHashTable[R][C] = K;
4.end
5.else
a.h= computeHashCode (K);
b.if BackupTable[h] is empty then
i.BackupTable[h] = Key;
ii.end
c.else
i.Perform Specified Probing and Store Key;
ii.end
6.end
Procedure: search (Key K);
1.R= computeRow(K);
2.C= computeCol(K);
3.if MatrixHashTable[R][C]==K then
a.return true;
4.end
5.else
a.h = computeHashCode (K);
b.if BackupTable[h]==K then
i.return true;
ii.end
c.else
i.Perform Specified Probing and Search Key;
ii.If the Key is found return true;
d.end
6.end
5.3. Prediction of Collision using Binomial Distribution
Probability theory can be used to predict collisions in a hash table. Consider a hash table with N locations. A specific location, A, is randomly selected among these N locations. A hash function H is also randomly chosen, and H (K) is computed for a key K. The computed H (K) will be equal to A with probability or will map to some other location with probability . Assuming there are D keys to be distributed across N locations in the table, the probability p(K) represents the likelihood of a collision of k keys at location A. Using the binomial distribution, p(K) is calculated as:
Probability, p(0) indicates that no key is mapped to the location A. Poisson distribution can be applied to compute p(K) in a better way as:
Equation (4) can be expressed in terms of load factor (λ) as .
5.4. Performance Analysis: Space Complexity and Time Complexity
This section briefly discusses space complexity and time complexity.
5.4.1. Space Complexity
The space complexity of different data structures can only be meaningfully compared if a common metric is used. In this work, we standardize the hash table size as P. Cuckoo Hashing assigns two hash tables of size P, resulting in a space complexity of O(2P). The Even-Odd hash function distributes 64 % of the load based on a Key Per Bucket (KPB) value of 32, and to maintain consistency, each row in the matrix hash table has the same number of columns. Thus, the matrix size is set to 32771×32. The space complexity of Matrix hashing is O(C1P), where C1 is a constant, valued at 1.01. Keys are placed in the matrix according to their computed hash codes, while keys that experience collisions are stored in the Backup table, with a size of O(C2P) where C2 is a constant valued at 0.49. Therefore, the total space complexity of the proposed scheme is O(C3P), with C3=1.5. Overall, the proposed scheme offers space efficiency that is 1.3 times better than Cuckoo Hashing.
Lemma1: Cuckoo Hashing does not offer the load factor of 0.5.
Proof: Let the total number of keys be n. The size of a hash table is (n+x) (as per the size of hash tables in both versions of Cuckoo Hashing); that is, the hash table is larger than the total number of keys. Load factor (λ) is the «ratio of total number of keys stored to the total number of locations offered in the hash table(s)». The load factor λ =f (n). Cuckoo Hashing Scheme uses two hash tables thus, . As x > 0 thus the load factor is less than 0.5.
5.4.2. Time Complexity
Performance of Cuckoo Hashing is dependent on its implementation i.e. whether it is running in a parallel environment or not. Performance of Cuckoo Hashing is dependent on the order of the lookup operation. By definition, Cuckoo Hashing is using two tables: T1 and T2 and two hash functions from the family of Universal hash functions. Universal hash function reports data loss of a key with probability of (1/n) if given universe of keys, U has size n.
Theorem 1: Cuckoo Hashing is dependent on the order of lookup operation.
Proof: Let P1 and P2 represent the probabilities of finding a key in tables T1 and T2, respectively, with a key being stored in only one table. In their analysis, the authors assume that Cuckoo Hashing does not result in data loss, so P1=1−P2.Cuckoo Hashing places each key at its computed hash code location, requiring only a single probe to verify the key’s presence in a table. If the cost of a single probe is denoted as t, the estimated total search cost, Ttotal, when starting with T1, can be calculated as: Ttotal=P1×t+P2×(t+t)=P1×t+2×(1−P1)×t=t×(2−P1).Thus, Ttotal is t×(2−P1) when the lookup operation begins with T1. If the lookup begins with T2, then Ttotal=t×(2−P2). Since P1≠P2 Ttotal varies and it depends on the order of the lookup.
Theorem 2: Matrix Hashing performs searching in constant time.
Proof: In the proposed approach, random probing is used exclusively in the backup table. The search time is directly proportional to the average search length. In the Matrix hash table, the average search length is 1, resulting in a search cost of t (the cost of a single probe). In the backup table, however, the average search length is given by (−1/λ) (ln(1−λ)), where λ represents the load factor of the backup table. The probabilities of finding a key in the Matrix hash table and the backup table are ϕ1 and ϕ2, respectively, with ϕ2=1−ϕ1. Thus, the estimated search cost for a key in Matrix Hashing can be calculated as follows: ϕ1×t+ϕ2×((−1/λ)ln(1−λ))×(2t). Since λ, ϕ1, and ϕ2 are constant for a given set of keys in the backup table, the search cost for a key in Matrix hashing is therefore constant.
6. Results and Discussion
This section evaluates the performance of the proposed Matrix Hashing scheme compared to Cuckoo Hashing. The evaluation considers several performance metrics: Search Time, Insertion Latency, Dexterity Degree, Memory Utilization, Average Search Time, Collision Rate, and Data Loss. The authors implemented three variants of quadratic probing in the backup table: conventional quadratic probing (QP), quadratic probing with prime numbers (QPP), and quadratic probing with Fibonacci numbers (QPF). Accordingly, MHQP represents Matrix Hashing with QP, MHQPP represents Matrix Hashing with QPP, and MHQPF represents Matrix Hashing with QPF. Additionally, random probing using prime numbers was implemented in the backup table and is denoted as MHRPP. Each Matrix Hashing variant underwent 20 iterations to retrieve all stored 10^6 keys from both tables. The experiments were conducted using a dataset of 10^6 purely random numbers from on an i7 processor running at 3.40 GHz, with 8 GB of DRAM on Ubuntu Linux 22.04.1. The dataset consists of 15-digit keys (Bozsolik, 2019). The clock() function from time.h was used to measure time consumption.
6.1. Performance of Even-Odd Hash Function
The primary goal of the Even-Odd hash function is to achieve an even distribution of load across buckets. This function determines the number of buckets based on the digit length of each key. In this study, the authors used random keys, each 15 digits long, totaling 106 keys. A total of 32,771 buckets were chosen—a prime number close to 215—to optimize distribution. As outlined in Contribution 2, the Even-Odd hash function effectively achieves an even load distribution, with approximately 64.5 % of keys placed across both hash tables according to the KPB (Key per Bucket). Figure 11 illustrates this balanced load distribution, highlighting the effectiveness of the proposed Even-Odd hash function in line with KPB metrics. Performance of Even-Odd hash function is shown in Figure 6.
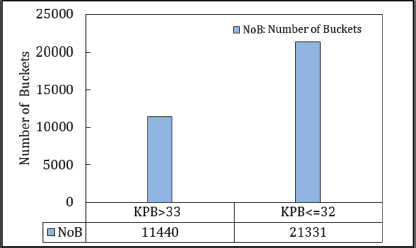
Figure 6. Performance of Even-Odd Hash Function
6.2. Matrix Hashing with Random Probing in 1D Array
The main objective of these experiments is to assess the impact of Matrix Hashing with Random Probing in a 1D Array on the specified performance metrics.
6.2.1. Searching Time
Search time is influenced by the average search length, which is minimized in the Matrix hash table as all keys are stored at their computed hash locations, resulting in an average search length of 1. When probing is necessary, however, the average search length increases. Among various probing techniques, the one with the shortest average search length is generally preferred. In the experimental setup, keys were first stored in the Matrix hash table, with any unpositioned keys then placed in a backup table. The search time for each iteration was averaged to calculate the Average Search Time (AST). Figure 7 illustrates the AST for each variant, with MHRPP demonstrating superior performance over other approaches.
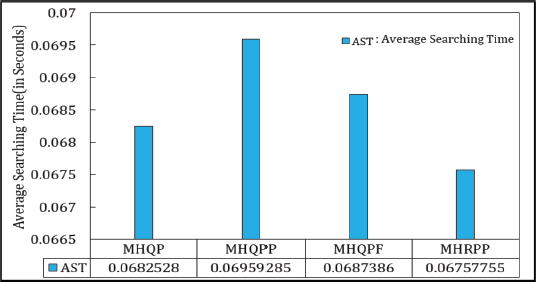
Figure 7. Average Search Time (AST) in Matrix Hashing
6.2.2. Insertion Latency
This is the time required to store keys in the hash table. The average search length directly affects the efficiency of the insertion process. The insertion latency for all variants is displayed in Figure 8.
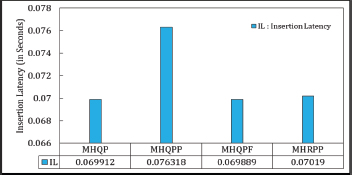
Figure 8. Insertion Latency (IL) in Matrix Hashing
6.2.3. Degree of Dexterity
This proposed performance indicator is defined as the reciprocal of the sum of search time and insertion latency, serving as a measure of hashing scheme efficiency. In this study, the authors used the average search time (AST), making the degree of dexterity (η) a function of both AST and insertion latency. A hash function with a higher η value is considered superior to others. The η values are shown in Figure 9, where MHRPP outperforms other variants in terms of η.
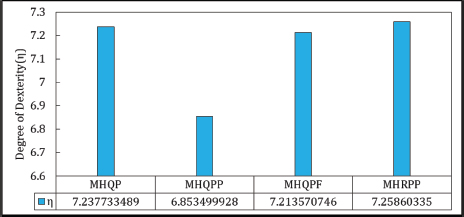
Figure 9. Degree of Dexterity (DoD) in Matrix Hashing
6.2.4. Keys at Home Location
Another key performance indicator used to compare the performance of MHQP, MHQPP, MHQPF, and MHRPP is Keys at Home Location (KAHL). The Matrix, as the primary table, stores 64.4858 % of all keys directly at their computed hash locations, while the remaining 355,142 keys are transferred to the backup table. KAHL is therefore identified as a crucial metric in evaluating performance. Among the variants, MHRPP accommodates more keys at their designated locations compared to MHQP, MHQPP, and MHQPF. Figures 10 and 11 illustrate the distribution of keys at home and other locations.
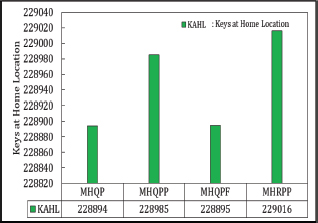
Figure 10. KAHL in Matrix Hashing
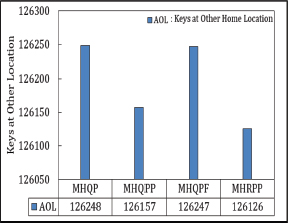
Figure 11. AOL in Matrix Hashing
6.2.5. Collision Rate
The next performance indicator is analysed using actual data from the experiment. In this study, the authors used D = 10ˆ6 keys with a hash table size of N=1,048. In the primary table, 356,033 keys remain unpositioned, yielding p(0)=0.385361. The theoretical number of unused locations in the primary table is then N×p(0)=1,048,583×0.385361=404.The actual unused locations in the primary table are calculated by subtracting the total number of positioned keys from the table size: (1,048,583−(1,000,000−356,033))=404,616. This results in a deviation of only 0.13 % between theoretical and actual values, indicating that the approximation is very close to the actual findings. Since the load factors (λ) of the primary and backup tables remain constant, the collision rates for MHQP, MHQPP, MHQPF, and MHRPP are identical. Figure 12, illustrates the collision rate across these variants.
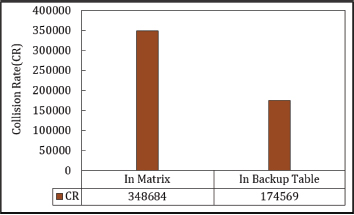
Figure 12. Collision Rate in Matrix Hashing
6.3. Experimental Results on Cuckoo Hashing
During the trials, a wide range of MaxLoop (ML) values was explored. For Symmetric Cuckoo Hashing, the ML range spans from ML=10 to ML=220 with increments of 10, while for Asymmetric Cuckoo Hashing, the ML range extends from ML=10 to ML=95 with increments of 5. The performance of Symmetric and Asymmetric Cuckoo Hashing was evaluated based on the following metrics: 1) Data Loss, 2) Data Collision, 3) Collision Rate 4) Average Searching Time, 5) Insertion Latency, 6) Degree of Dexterity, and 7) Memory Usage.
6.3.1. Data Loss
Data loss in both Symmetric and Asymmetric Cuckoo Hashing is influenced by the MaxLoop (ML) value. At ML=200, Symmetric Cuckoo Hashing experiences only a single key loss, while Asymmetric Cuckoo Hashing demonstrates no data loss at ML=95. This suggests that increasing ML can effectively reduce data loss in both hashing methods, as illustrated in Figures 13 and 14. The probability of data loss predicted by Universal Hash Functions is for keys within a universe U of size |U|=m. This result is achieved without requiring costly rehash operations, as seen with Symmetric Cuckoo Hashing at ML=200 and Asymmetric Cuckoo Hashing at ML=95. The authors recommend using a stash for cases of insertion failure in Cuckoo Hashing, as higher ML values tend to decrease data loss (Kirsch and Mitzenmacher, 2010). Thus, introducing a small stash can effectively manage insertion failures.
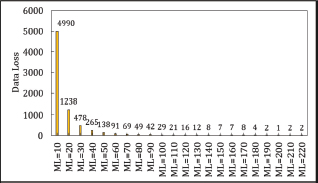
Figure 13. Data Loss in Symmetric Cuckoo Hashing
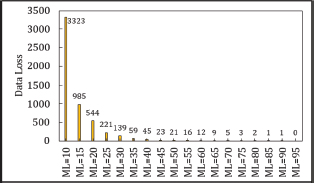
Figure 14. Data Loss in Symmetric Cuckoo Hashing
6.3.2. Data Collision
Data collisions in both Symmetric and Asymmetric Cuckoo Hashing are analyzed using the model outlined in Section 5.1. The number of data collisions identified by this model is used to calculate collision rates. Figures 15 and 16 present the data collisions and collision rates for both hashing methods. In terms of data collisions and collision rate, Asymmetric Cuckoo Hashing outperforms Symmetric Cuckoo Hashing.
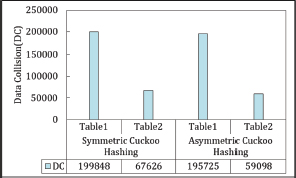
Figure 15. Data Collision in Symmetric Cuckoo Hashing and Asymmetric Cuckoo Hashing
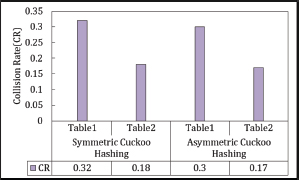
Figure 16. Collision Rate in Symmetric Cuckoo Hashing and Asymmetric Cuckoo Hashing
6.3.3. Average Searching Time
An inconsistent relationship is observed between MaxLoop (ML) and the average search time (AST) in both Asymmetric and Symmetric Cuckoo Hashing algorithms. Figures 17, 18, 19 and 20 show that ML does not impact the average search time in Asymmetric Cuckoo Hashing. Figure 21 further illustrates the AST for Symmetric Cuckoo Hashing at ML=200 and Asymmetric Cuckoo Hashing at ML=95. These findings suggest that both hashing methods achieve improved performance when searches are biased towards Table 2.
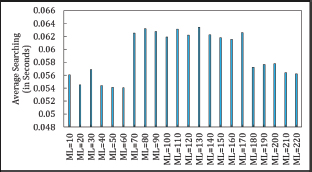
Figure 17. Average searching Time in Symmetric Cuckoo Hashing When Searching Starts from Table1
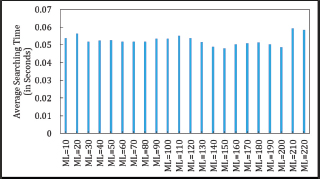
Figure 18. Average searching Time in Symmetric Cuckoo Hashing When Searching Starts from Table2
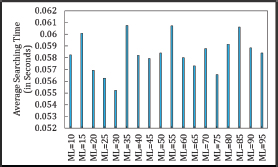
Figure 19. Average searching Time in Asymmetric Cuckoo Hashing When Searching Starts from Table1
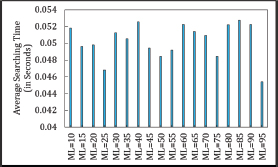
Figure 20. Average searching Time in Asymmetric Cuckoo Hashing When Searching Starts from Table2
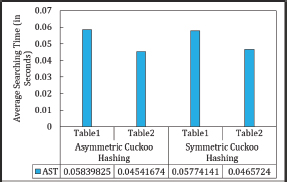
Figure 21. Average searching Time in Asymmetric Cuckoo Hashing When Searching Starts from Table2
6.3.4. Insertion Latency
Insertion latency (IL) remains unaffected by the MaxLoop (ML) value in both Asymmetric and Symmetric Cuckoo Hashing, as illustrated in Figures 22, 23, 24, and 25.
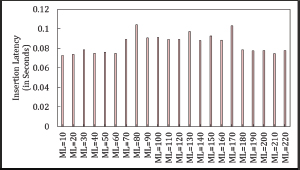
Figure 22. Insertion Latency in Symmetric Cuckoo Hashing When Searching Starts from Table1
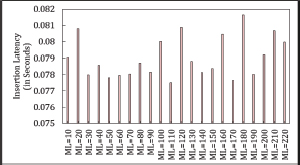
Figure 23. Insertion Latency in Symmetric Cuckoo Hashing When Searching Starts from Table2
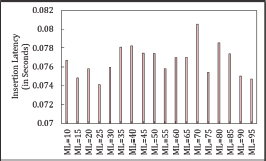
Figure 24. Insertion Latency in Asymmetric Cuckoo Hashing When Searching Starts from Table1. Hashing When Searching Starts from Table1
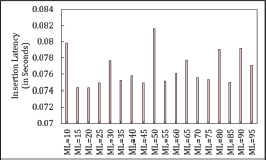
Figure 25. Insertion Latency in Asymmetric Cuckoo Hashing When Searching Starts from Table2
Figure 26 specifically presents the insertion latency at ML=200 for Symmetric Cuckoo Hashing and ML=95 for Asymmetric Cuckoo Hashing.
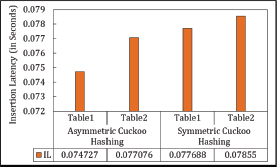
Figure 26. Insertion Latency in Symmetric Cuckoo (at ML=200) Hashing and Asymmetric Cuckoo Hashing (at ML=95)
6.3.5. Degree of Dexterity
The Degree of Dexterity (η) depends on both the Average Searching Time (AST) and Insertion Latency (IL). Given that ML does not affect either AST or IL, η is also independent of ML. Figure 27 displays the η values for both Asymmetric and Symmetric Cuckoo Hashing.
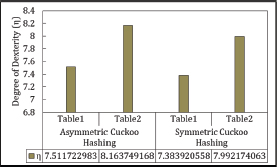
Figure 27. Degree of Dexterity in Symmetric Cuckoo Hashing (at ML=200) and Asymmetric Cuckoo Hashing (at ML=95)
6.3.6. Memory Usages
Data loss is influenced by ML, and memory usage increases as ML rises, as illustrated in Figures 28, 29, and 30. The highest memory usage occurs at ML=200 for Symmetric Cuckoo Hashing and ML=95 for Asymmetric Cuckoo Hashing, as shown in Figure 27. For this trial, the hash table sizes were set to 1,000,033 and 1,099,997 for Asymmetric Cuckoo Hashing. Notably, one hash table should be more than twice the size of the other, as initially recommended by the creators of Cuckoo Hashing. Following this guideline, the authors also tested with table sizes of 1,000,033 and 2,000,081. During the trial, only insertion latency showed improvement, reaching 0.064015 seconds at ML=95 in Asymmetric Cuckoo Hashing, while average searching time remained unchanged.
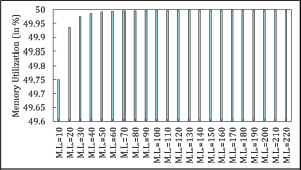
Figure 28. Memory Utilization in Symmetric Cuckoo Hashing
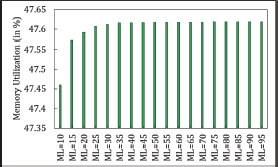
Figure 29. Memory Utilization in Asymmetric Cuckoo Hashing
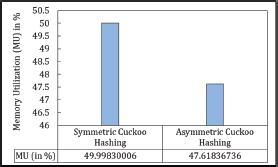
Figure 30. Memory Utilization in Symmetric Cuckoo Hashing (at ML=200) and Asymmetric Cuckoo Hashing (at ML=95)
6.4. Comparison: Cuckoo Hashing and Matrix Hashing with Random Probing in 1D Array
6.4.1. Average Searching Time
The average search time of Asymmetric Cuckoo Hashing is shorter than that of the other two methods. However, Symmetric Cuckoo Hashing competes closely with Asymmetric Cuckoo Hashing in terms of average search time. In the proposed scheme, the worst-case performance—where the search begins in Table 1—is 0.009 seconds slower than both variants of Cuckoo Hashing. The average search times are displayed in Figure 31.
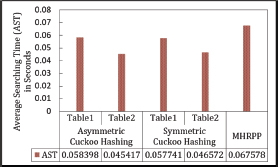
Figure 31. Average Searching Time in Asymmetric Cuckoo Hashing, Symmetric Cuckoo Hashing and Matrix Hashing (MHRPP)
6.4.2. Insertion Latency Time
In terms of insertion latency, the proposed scheme is 0.006 seconds faster than Asymmetric Cuckoo Hashing and 0.007 seconds faster than Symmetric Cuckoo Hashing in the best-case scenario. The insertion latencies are illustrated in Figure 32.
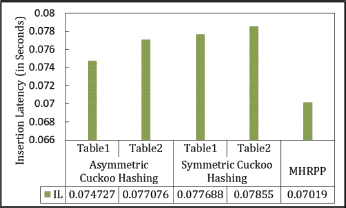
Figure 32. Insertion Latency in Asymmetric Cuckoo Hashing, Symmetric Cuckoo Hashing and Matrix Hashing (MHRPP)
6.4.3. Degree of Dexterity
The proposed scheme outperforms Cuckoo Hashing in terms of insertion latency, resulting in a lower η value compared to both versions of Cuckoo Hashing. However, under worst-case conditions, the proposed scheme is 25.3 % slower than Asymmetric Cuckoo Hashing and 12.5 % slower than Symmetric Cuckoo Hashing. Degree of Dexterity is shown in Figure 33.
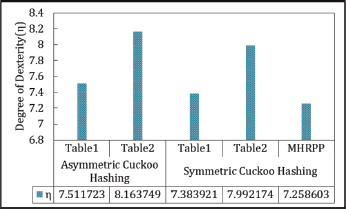
Figure 33. Degree of Dexterity in Asymmetric Cuckoo Hashing, Symmetric Cuckoo Hashing and Matrix Hashing (MHRPP)
6.4.4. Memory Usages
The proposed scheme outperforms both Asymmetric and Symmetric Cuckoo Hashing. It achieves a memory usage rate of 64.5 %, whereas Cuckoo Hashing fails to reach even 50 % memory utilization.
Memory utilization (in %) is shown in Figure 34.
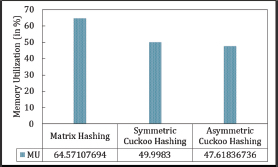
Figure 34. Memory Utilization in Asymmetric Cuckoo Hashing, Symmetric Cuckoo Hashing and Matrix Hashing (MHRPP)
7. Conclusion and Future Scope
Cuckoo Hashing is a hashing technique designed to address challenges commonly encountered in traditional methods, such as chaining and linear probing. However, three primary challenges are associated with Cuckoo Hashing itself: inefficient memory usage, high insertion latency, and significant data migration costs. These issues are well-documented in the literature, and researchers have proposed various optimizations to mitigate them. These include using more effective hash functions, implementing dynamic resizing strategies, and developing hybrid approaches that combine Cuckoo Hashing with other techniques to improve overall performance.
The proposed Even-Odd hash function, inspired by Combinatorial Hashing, aims to reduce computational cost and achieves a 64.5 % success rate in placing keys directly in their «home» locations. This hash function has been implemented in a prototype called Matrix Hashing in this study. In Matrix Hashing, prime numbers and Fibonacci numbers are applied in quadratic and random probing techniques.
Matrix Hashing is evaluated against both the Asymmetric and Symmetric versions of Cuckoo Hashing. In terms of average search time, Matrix Hashing lags behind Symmetric and Asymmetric Cuckoo Hashing by 0.009 seconds. However, it demonstrates a 0.006-second advantage in insertion latency under worst-case scenarios. Matrix Hashing also shows improved memory utilization at 64.57 %, compared to Cuckoo Hashing’s sub-50 % memory efficiency. However, Matrix Hashing’s «Degree of Dexterity» is 25 % lower than that of Symmetric and Asymmetric Cuckoo Hashing, due to the latter’s faster average search times. While Cuckoo Hashing suffers from data migration costs, Matrix Hashing eliminates this issue entirely.
The performance of Chaining, on the other hand, largely depends on the lengths of the linked lists within each bucket, with uneven load distribution posing a significant challenge. By integrating the Even-Odd hash function into Chaining, researchers may improve load distribution across buckets, potentially enhancing Chaining’s overall performance. The Even-Odd hash function thus offers a promising approach for optimizing Chaining.
References
Awad, M. A., Ashkiani, S., Porumbescu, S. D., Farach-Colton, M., & Owens, J. D. (2023). Analyzing and Implementing GPU Hash Tables. 2023 Symposium on Algorithmic Principles of Computer Systems (APOCS), 33–50. https://doi.org/10.1137/1.9781611977578.ch3.
Bai, X., Yang, H., Zhou, J., Ren, P., & Cheng, J. (2014). Data-dependent hashing based on p-stable distribution. IEEE Transactions on Image Processing, 23(12), 5033–5046. https://doi.org/10.1109/TIP.2014.2352458.
Balasundaram, R., & Sudha, G. F. (2021). Retrieval performance analysis of multibiometric database using optimized multidimensional spectral hashing-based indexing. Journal of King Saud University – Computer and Information Sciences, 33(1), 110–117. https://doi.org/10.1016/j.jksuci.2018.02.003.
Bozsolik, T. (2019). Random numbers. https://www.kaggle.com/code/timoboz/a-lot-of-random-numbers. https://doi.org/10.34740/KAGGLE/DSV/816507.
Cai, D. (2021). A Revisit of Hashing Algorithms for Approximate Nearest Neighbor Search. IEEE Transactions on Knowledge and Data Engineering, 33(6), 2337–2348. https://doi.org/10.1109/TKDE.2019.2953897.
Carter, J. L., & Wegman, M. N. (1979). Universal classes of hash functions. Journal of Computer and System Sciences, 18(2), 143–154. https://doi.org/10.1016/0022-0000(79)90044-8.
Chi, L., & Zhu, X. (2017). Hashing techniques: A survey and taxonomy. ACM Computing Surveys (CSUR), 50(1), 1–36. https://doi.org/10.1145/3047307.
Debnath, B. K., Sengupta, S., & Li, J. (2010). ChunkStash: Speeding Up Inline Storage Deduplication Using Flash Memory. USENIX Annual Technical Conference, 1–16.
Fan, B., Andersen, D. G., & Kaminsky, M. (2013). Memc3: Compact and concurrent memcache with dumber caching and smarter hashing. In 10th USENIX Symposium on Networked Systems Design and Implementation (NSDI 13), 371–384.
Fang, S.-H., Fei, Y.-X., Xu, Z., & Tsao, Y. (2017). Learning transportation modes from smartphone sensors based on deep neural network. IEEE Sensors Journal, 17(18), 6111–6118. https://doi.org/10.1109/JSEN.2017.2737825.
Ferdman, M., Lotfi-Kamran, P., Balet, K., & Falsafi, B. (2011). Cuckoo directory: A scalable directory for many-core systems. In 2011 IEEE 17th International Symposium on High Performance Computer Architecture, 169–180. https://doi.org/10.1109/HPCA.2011.5749726.
García-Peñalvo, F., Vázquez-Ingelmo, A., García-Holgado, A., Sampedro-Gómez, J., Sánchez-Puente, A., Vicente-Palacios, V., Dorado-Díaz, P. I., & Sánchez, P. L. (2024). KoopaML: A Graphical Platform for Building Machine Learning Pipelines Adapted to Health Professionals. International Journal of Interactive Multimedia and Artificial Intelligence, 8(6), 112–119. https://doi.org/10.9781/ijimai.2023.01.006.
Guibas, L. J. (1978). The analysis of hashing techniques that exhibit k-ary clustering. Journal of the ACM (JACM), 25(4), 544–555. https://doi.org/10.1145/322092.322096.
Jiménez, A., Elizalde, B., & Raj, B. (2018). Acoustic scene classification using discrete random hashing for Laplacian kernel machines. In 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 146–150. https://doi.org/10.1109/ICASSP.2018.8461631.
Kirsch, A., & Mitzenmacher, M. (2010). More robust hashing: Cuckoo Hashing with a stash. SIAM Journal on Computing, 39(4), 1543–1561. https://doi.org/10.1137/080728743.
Kurpicz, F., Lehmann, H.-P., & Sanders, P. (2023). Pachash: Packed and compressed hash tables. In 2023 Proceedings of the Symposium on Algorithm Engineering and Experiments (ALENEX), 162–175. https://doi.org/10.1137/1.9781611977561.ch14.
Larson, P. (1983). Analysis of uniform hashing. Journal of the ACM (JACM), 30(4), 805–819. https://doi.org/10.1145/2157.322407.
Liang, X., & Wang, G. (2017). A convolutional neural network for transportation mode detection based on smartphone platform. In Proc. MASS, 338–342. https://doi.org/10.1109/MASS.2017.81.
Maurer, W. D., & Lewis, T. G. (1975). Hash table methods. ACM Computing Surveys (CSUR), 7(1), 5–19. https://doi.org/10.1145/356643.356645.
Minaud, B., & Papamanthou, C. (2023). Generalized Cuckoo Hashing with a stash, revisited. Information Processing Letters, 181, 106356. https://doi.org/10.1016/j.ipl.2022.106356.
Pagh, R. (2001). On the cell probe complexity of membership and perfect hashing. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, 425–432. https://doi.org/10.1145/380752.380836.
Pagh, R., & Rodler, F. F. (2004). Cuckoo Hashing. Journal of Algorithms, 51(2), 122–144. https://doi.org/10.1016/j.jalgor.2003.12.002.
Patel, F. S., & Kasat, D. (2017). Hashing based indexing techniques for content-based image retrieval: A survey. In 2017 International Conference on Innovative Mechanisms for Industry Applications (ICIMIA), 279–283. https://doi.org/10.1109/ICIMIA.2017.7975619.
Pontarelli, S., Reviriego, P., & Mitzenmacher, M. (2018). Emoma: Exact match in one memory access. IEEE Transactions on Knowledge and Data Engineering, 30(11), 2120–2133. https://doi.org/10.1109/TKDE.2018.2818716.
Shi, S., & Qian, C. (2020). Ludo hashing: Compact, fast, and dynamic key-value lookups for practical network systems. Proceedings of the ACM on Measurement and Analysis of Computing Systems, 4(2), 1–32. https://doi.org/10.1145/3392140.
Skarlatos, D., Kokolis, A., Xu, T., & Torrellas, J. (2020). Elastic Cuckoo Page Tables: Rethinking Virtual Memory Translation for Parallelism. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’20, 1093–1108. https://doi.org/10.1145/3373376.3378493.
Stevens, H. (2018). Hans Peter Luhn and the birth of the hashing algorithm. IEEE Spectrum, 55(2), 44–49. https://doi.org/10.1109/MSPEC.2018.8278136.
Sun, Y., Hua, Y., Feng, D., Yang, L., Zuo, P., Cao, S., & Guo, Y. (2016). A Collision-mitigation Cuckoo Hashing scheme for large-scale storage systems. IEEE Transactions on Parallel and Distributed Systems, 28(3), 619–632. https://doi.org/10.1109/TPDS.2016.2594763.
Suruliandi, T., Idhaya, S., & Raja, P. (2024). Drug Target Interaction Prediction Using Machine Learning Techniques – A Review. International Journal of Interactive Multimedia and Artificial Intelligence, 8(6), 86–100. https://doi.org/10.9781/ijimai.2022.11.002.
Vitter, J. S. (1983). Analysis of the search performance of coalesced hashing. Journal of the ACM (JACM), 30(2), 231–258. https://doi.org/10.1145/322374.322375.
Wu, Y., Liu, Z., Yu, X., Gui, J., Gan, H., Han, Y., Li, T., Rottenstreich, O., & Yang, T. (2021). MapEmbed: Perfect Hashing with High Load Factor and Fast Update. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, KDD ’21, 1863–1872. https://doi.org/10.1145/3447548.3467240.
Wu, X., Zhu, X., & Wu, M. (2022). The Evolution of Search: Three Computing Paradigms. ACM Transactions on Management Information Systems (TMIS), 13(2). https://doi.org/10.1145/3495214.