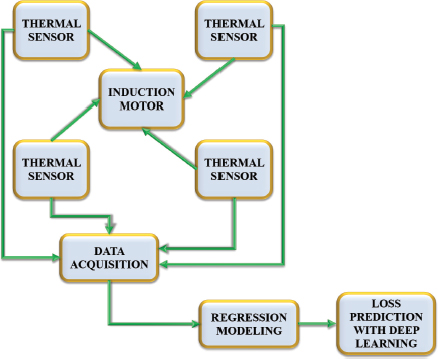
Figure 1. Process Flow Diagram
ADCAIJ: Advances in Distributed Computing and Artificial Intelligence Journal
Regular Issue, Vol. 11 N. 3 (2022), 349-365
eISSN: 2255-2863
DOI: https://doi.org/10.14201/adcaij.28435
Regression Based Performance Analysis and Fault Detection in Induction Motors by Using Deep Learning Technique
Pradeep Kattaa, Karunanithi Kandasamyb, Raja Soosaimarian Peter Rajc, Ramesh Subramaniand, and Chandrasekar Perumale
a Research Scholar, School of Electrical and Communication Engineering, Vel Tech Rangarajan Dr.Sagunthala R&D Institute of Science and Technology, Chennai, Tamilnadu, India
b,d,e Professor, School of Electrical and Communication Engineering, Vel Tech Rangarajan Dr.Sagunthala R&D Institute of Science and Technology, Chennai, Tamilnadu, India
c Associate Professor, School of Computer Science and Engineering, Vellore Institute of Technology, Vellore, Tamilnadu, India
✉ pradeep.2048@gmail.com, k.karunanithiklu@gmail.com, avemariaraja@gmail.com, rameshsme@gmail.com, drchandrasekar@veltech.edu.in
ABSTRACT
The recent improvements related to the area of electric locomotive, power electronics, assembly processes and manufacturing of machines have increased the robustness and reliability of induction motors. Regardless of the increased availability, the application of induction motors in many fields alleges the need for operating state supervision and condition monitoring. In other words, fault identification at the initial stage helps make appropriate control decisions, influencing product quality as well as providing safety. Inspired by these demands, this work proposes a regression based modeling for the analysis of performance in induction motors. In this approach, the feature extraction process is combined with classification for efficient fault detection. Deep Belief Network (DBN) stacked with multiple Restricted Boltzmann Machine (RBM) is exploited for the robust diagnosis of faults with the adoption of training process. The influences of harmonics over induction motors are identified and the losses are mitigated. The simulation of the suggested approach and its comparison with traditional approaches are executed. An overall accuracy of 99.5% is obtained which in turn proves the efficiency of DBN in detecting faults.
KEYWORDS
induction motor; DBN; RBM; Fast Fourier Transform (FFT); regression modeling
1. Introduction
Induction motors (IM) are regarded as the major load in electric power systems and contributes to half of the electric energy demand consumed globally (Donolo et al., 2020). These motors are incorporated equipment which are generally utilized in industrial applications and manufacturing processes. The proper functioning of IMs is mandatory for the effective functioning of industries. In contrast, numerous faults occur frequently in Ims because of enduring or overrated loads, tough working conditions, regular wear and tear as well as unexpected events. This requires an efficient fault detection approach to prevent shutdown, unsafe operation, repair as well as operational costs and catastrophic failures (Liu et al., 2017). Moreover, IMs are subjected to numerous power quality problems like imbalance, fluctuations and disturbances in voltage. Additional losses occur when IMs are supplied with voltage of decreased quality. This further results in decreased efficiency and overheating (Ghaseminezhad et al., 2017; Amaize et al., 2017).
Generally, under conditions where voltage is unbalanced, the equivalent induction motor circuit is separated into negative and positive sequence equivalent circuits. The distorted waveform of voltage obtained during this condition has large harmonic components which further performs distortion of current and flux density waveforms in the induction motor. This results in the efficiency being compromised and in complicated loss characteristics during distorted as well as unbalanced voltage conditions. The analysis of induction motor loss considers namely, the rotor electromagnetic quantity harmonics have to initially identified. At partial-load condition, in the induction motor, the fundamental frequency of the rotor is less than 1 Hz. This signal of reduced frequency comprises of numerous power supply cycles incurring greater calculation cost. Hence, rapid analysis of induction motor loss characteristics is tedious. Secondly, iron loss prediction is complicated in an induction motor due to the magnetic material characteristics which are nonlinear in nature. A finite element model (FEM) which exhibits extensive improvements, is applied to an induction motor to determine loss. Unfortunately, the theoretical study related to distortion and voltage imbalance on induction motor loss properties is not sufficient (Zhang et al., 2018). Hence, regression based analysis is exploited in this work which solves the power quality issues and mitigates the induction motor losses.
In induction motors, fault detection is important to maintain the efficient functioning of industrial process without interruption (Ali et al., 2019). The three basic approaches for fault detection in induction motors are mentioned as follows: i) the signature extraction based approach (Hassan et al., 2018) is performed by the survey of fault signatures in frequency or time domain. This approach requires more advanced tools for signal processing.
ii) The model based approach (Su et al., 2017) depends on mathematical modeling for predicting induction motor behaviour during fault conditions. Even though this approach generates warnings as well as determines incipient faults, the accuracy depends largely on explicit motor types which are scarcely available. iii) The knowledge based approach (Xu et al., 2017) does not require characteristics of motor or load, trigger threshold and machine models. On the contrary, this approach demands thorough data analysis to generate effective rules or inferences for fault detection. The Discrete Wavelet Transform (DWT) approach (Bessous et al., 2018),(Ghods et al., 2016; Nishat Toma et al., 2020) performs efficiently with increased power motors during steady-state circumstances including constant torque, speed and voltage. It identifies the harmonics thereby distinguishing the induction motor faults during steady state. In contrast, with non-stationary signals, the deterioration of spectrum occurs, resulting in information loss of fault diagnosis. Moreover, the DWT based approach depends heavily on the quality of the measurement, the number of samples taken as well as sampling frequency. Henceforth, to improvise the monitoring and diagnostic performance of an induction motor, machine learning approaches are opted. Few of them are Random forest (Ma et al., 2018), Support Vector Machine (Pandarakone et al., 2016), K-nearest neighbour (Dong et al., 2016), Decision Tree (Toma et al., 2020) and Naive Bayes classifier (Zhang et al., 2018).
The adoption of these Machine Learning (ML) approaches results in decreased reliability due to more missing data. The introduction of deep learning approaches addresses these shortcomings and generates acceptable and promising results related to fault diagnosis in induction motors. These approaches utilized manually extracted features (Abid et al., 2019). Some of the merits of deep learning approaches over ML approaches are as follows: versatility to be trained for any type of utility, reduced computation time as well as parameter tuning in the absence of programming skill. Among the deep learning approaches, Convolutional Neural Networks (CNN) is utilized for the diagnosis of faults but did not provide the deep analysis (Ding et al., 2017; Hsueh et al., 2019).
Considering the above discussed factors, this work contributes an approach based on deep learning for the mitigation of losses and fault detection in induction motors. A regression based analysis is performed for estimating the power factor at varying load because reduced power factor generates huge losses in induction motor. The DBN comprising of RBM is adopted for the attainment of fault detection in induction motors with improved classification accuracy. The remaining paper is structured as follows: Section overviews related works, Section 3 presents the proposed approach, Section 4 outlines the results and a discussion, Section 5 draws conclusions from the conducted research.
2. Related Work
Prashant Kumar and Ananda Shankar Hati (Kumar et al., 2021) have introduced an adaptive gradient optimizer based deep convolutional neural network (ADG-dCNN) approach for finding the faults occurring in the rotor and bearing of squirrel cage induction motor. By this approach, human expertise requirement is highly reduced and the feature extraction process is enabled automatically. For fault detection, vibration data from numerous MEMS accelerometers are gathered. Here, SHapley Additive exPlanations (SHAP) technique has been implemented for evaluating fault classification. It is difficult to carry out multiple fault detection since a large amount of data is required in order to achieve high fault categorization accuracy.
R. R. Kumar et al (2021) have proposed a new technique for identifying and categorising faults in an induction motor with the help of a two stage Neural Network (NN). Here all data are represented by using Principle Component Analysis (PCA) which is a linear-based feature reduction method. The three- phase current signals are detected and classified online using shallow neural networks. Overfitting inhibits the generalization capacity.
S. M. K. Zaman et al (2021) have introduced a Graph-based Semi Supervised Learning (GSSL) method for identifying the faults that occur in a direct online induction motor. The prominent advantage of GSSL is that the training datasets require a lower number of labelled data. The Greedy-Gradient Max Cut (GGMC) algorithm from the GSSL family has been used in this research to analyse the compatibility of this approach. Obtaining a huge labelled training dataset is quite costly, difficult and time consuming.
A. Chouhan et al (2021) have developed an effective Artificial Neural Network (ANN) model for predicting both electrical and mechanical faults in an induction motor, which is operated at three different conditions: same speed, interpolated speed and extrapolated speed. A machinery fault stimulator is utilized to measure the current and vibration signals of healthy and faulty induction motors. This fault detection technique is more accurate in interpolation speed cases than extrapolation speed cases.
A. Ibrahim et al (2022) have proposed a novel Hybrid Invasive Weed Optimization (IWO) method for the detection of induction-motor faults. An optimal features selection process was implemented and machine learning classifiers were trained to classify the faults. Here, fault identification had not been carried out at the early stage by taking into account the current and vibration signal.
3. Proposed Approach
The performance analysis as well as fault detection in induction motors have evolved as a significant area of interest. Numerous researches have been carried out in relation to the monitoring of induction motor operation and the early detection of faults. From among them, deep learning based approaches are regarded as efficient and in this paper, DBN comprising of multiple stacks of RBM has been utilized. The block diagram of the suggested approach is given in Figure 1.

Figure 1. Process Flow Diagram
The data from the induction motor at varying conditions of rotating speed has been obtained and subjected to regression analysis. It is utilized to estimate the appropriate power factor in order to mitigate the losses occurring in induction motors. Further, DBN has been adopted for the identification of faults with an improved training of RBM. In general, DBN comprises of multiple hidden layers with the ability to learn hierarchical representation in an unsupervised manner. It also performs classification and RBM is exploited to make the learning of abundant parameters easier.
3.1. Regression Modeling
Regression is regarded as a statistical approach utilized for the fitting of nonlinear as well as linear models. It denotes the relation between the independent variable p and the dependent variable q considering a nth degree polynomial. Regression involves two main factors, given as: Consideration of observed values to simulate a regression model and prediction of polynomial coefficients. The corresponding expression is given by,
Here, qi indicates observed dependent variable, f (pi, β) indicates predicted value, εi represents the error between the estimated and observed value. (β0, β1, β2, βm) are the polynomial coefficients in which m indicates the coefficient number. p1 + p22 + … pmn are independent variables in which m represents the polynomial degree number and n represents the number of variables. The difference between (1) and (2) provides the value of the mean square error. The sensors provided in the system perform observation of speed as well as motor torque. The power factor is obtained from the equation given below.
Here, V indicates the rms voltage, I is the rms current, PF represents the power factor, η denotes efficiency and Pin indicates input power at full rated load. Since the power factor of the induction motor is nonlinear, the regression model has been adopted to solve and determine the power factor value.
Figure 2 denotes the parameters measured including the power factor, total current, active current and reactive current. The load factor is estimated by equations (3) and (4) from which the power factor is calculated. It is clear that the power factor is low at minimized load condition because during this condition, the motor consumes only reactive current and the active current approximately equals zero. The active current increases with the increase in load which further results in the increase of the power factor. Hence, in conditions where load is reduced, the power factor has to be detected because low power factor results in losses. The regression based modeling is regarded as a solution of reduced cost for the determination of the power factor at varying load condition.
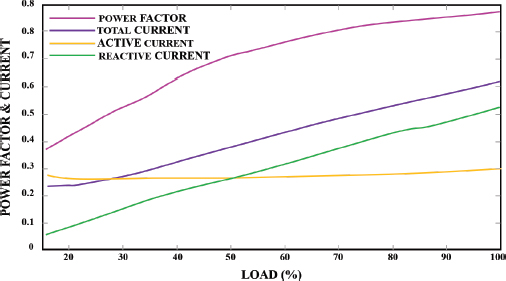
Figure 2. Measurement of the current and power factor
3.2. RBM Architecture and Training
The RBM is utilized as generative model of various data types including signal coefficients and performs learning approach for DBN. Usually, RBMs are trained utilizing the learning procedures which considers factors such as momentum, learning rate, number of hidden units, mini-batch size and initial value of weights. The architecture of RBM given in Figure 3 comprises a visible layer and a hidden layer. All the visible layer units are connected to the hidden layer units but the units are not interconnected. Considering the hidden and visible units, the energy of (v, h) is given by,
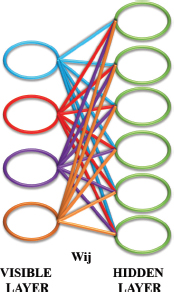
Figure 3. RBM architecture
Here, vi, hj denote visible unit as well as hidden unit binary states, xi and yi represent the biases, wij denote the weight between the binary states. A probability is assigned to each possible pair of hidden and visible layers through the function given by,
The partition function Z is given by,
Probability of assigning a network to the visible vector v is denoted by the summation of all hidden vectors which are possible.
The probability of assigning a network to a training data is increased with the adjustment of weights as well as biases for reducing energy of that specific data. This is followed by increasing the energy of other data, specifically data with reduced energy. The log probability derivative of training vector with respect to weight is given by,
The simple learning rule for the log probability of training data is given by,
Here ϵ denotes the learning rate. The unbiased sample of vihjdata is obtained easily due to the absence of direct connection within hidden units of RBM. When a training data v is selected randomly, the binary state hj of every hidden unit is set to 1 with probability given by,
Here, σ(a) indicates a logistic function 1/(1 + exp (−x))
Similarly, the unbiased sample of visible units is easily obtained due to the absence of direct connection between visible units.
To obtain an unbiased sample of vihjmodel, any random state of visible unit is initialized and Gibbs sampling is performed alternatively. A single iteration comprises of updating hidden unit using equation (11) subsequently followed by updating visible unit using equation (12).
3.3. DBN Architecture
DBN is a deep learning network comprising of numerous hidden layers with many nonlinear representations. This network is regarded as a probabilistic generative model in which multiple RBMs are stacked together as shown in Figure 4.
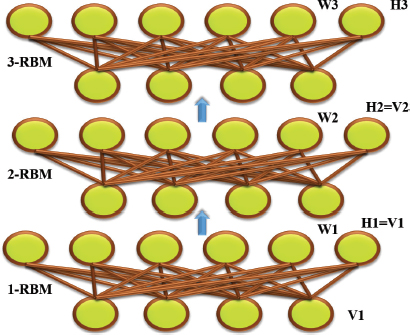
Figure 4. DBN architecture
Since, multiple hidden layers are present in DBN, the learning is carried out from input data and hierarchical representation related to every hidden layer is extracted. The joint distribution within l hidden layers hk and visible layer v is estimated as,
The method of learning a wide range of parameters utilizing conventional learning methods is tedious due to the transmission of errors to lower levels. Added to this, the ability for parameter adjustment is complicated resulting in difficulties for the generation of optimal parameters. Due to this, the following procedure is adopted for the training purpose: Initially, the hidden layer and input units are trained by the RBM rule. Next, the first hidden layer output is given to the second hidden layer input. Similarly all hidden layers are trained till the training of all hidden layers is completed.
3.4. DBN for Fault Diagnosis
A fault detection approach based on DBN comprising of RBM is proposed for induction motors as shown in Figure 5. DBN has been chosen due to its supervised learning and its ability to reduce training error with through improved classification accuracy.
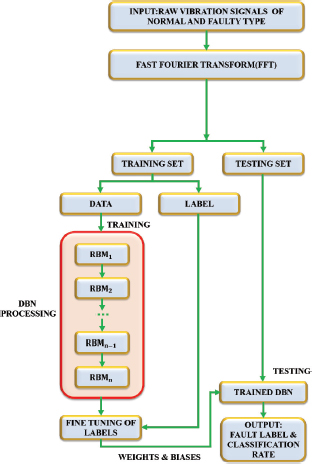
Figure 5. Fault detection approach based on DBN
Since the vibration signals contain significant information reflecting the working condition of induction motors, these signals are chosen as input signals. Due to the presence of correlation among sampled data points, the adjacent classification tasks get affected. To avoid this, the vibration signals are converted into frequency domain from time domain utilizing FFT. This conversion enables the evaluation of difference within constitutive frequency components and their distribution. In this work, an amplitude of 30Hz and 90Hz components is selected as features for the categorization of faults in induction motors. This is because, at the above mentioned frequencies, high difference in amplitude is obtained which differentiates the operating conditions of the induction motor. The feature location generally depends on the rotation speed of the induction motor. During analysis, no overlapping occurs and hence the faults are identified at the initial stage. Each of the obtained features is applied as input to the DBN architecture and the corresponding training process is explained below.
Step 1: Initialize the input parameters and input data set.
Step 2: Initialize the first layer for training such that i = 1.
Step 3: Train the first layer using the RBM learning rule.
Step 4: Save the obtained representations, biases and weights.
Step 5: Perform training till the completion of all layers.
Step 6: Following training, perform supervised learning for the classification of faults.
Step 7: Perform fine tuning of all parameters.
Thus, the DBN is exploited for efficient training of input data thereby providing accurate classified results in the detection of faults in induction motors. The deep network parameters are updated on the bases of learning rules for the generation of more accurate results.
4. Results and Discussion
The experimentation and simulation of the proposed approach considers an induction motor. The behavior of the motor related to different faults has been analysed utilizing the fast fourier transform. It converts the variations of stator current into domain and these features are treated for the deep learning approach for fault diagnosis and classification. The FFT feature dataset comprises three partitions: i) A set of 2400 data for training, fine tuning and testing. ii) A set of 800 data without fault types for training which has been utilized to perform forward stack-learning of RBM from input to high layers. iii) A set of 800 data with fault types has been used to investigate DBN’s recognition rate. It performs learning in backward fine-tuning manner from the classification layer to the low layers.
Figure 6 represents the waveform indicating the speed of the motor. The induction motor was made to operate in faulty conditions and the corresponding motor speed was retrieved. Subsequently, the power factor is estimated to determine losses and this is performed by regression modeling. In this approach, polynomial function is applied to obtain the power factor value with high accuracy.
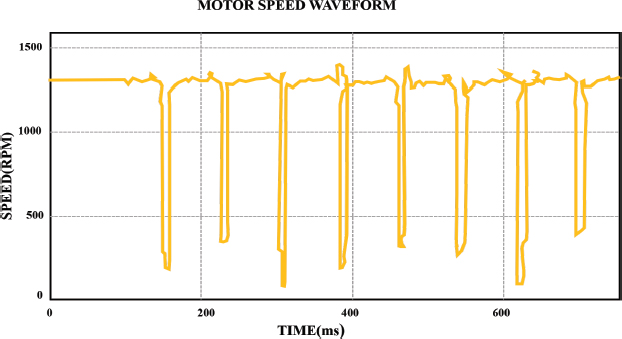
Figure 6. Waveform for motor speed
The coefficients of the polynomial are predicted and the unknown power factor values are determined. This approach provides improved performance with increased flexibility and reliability. The accuracy of the unknown estimation points is determined by the residual errors of set points. Figures 7 (a), 7 (b) and 7(c) represents the estimated power factor curve and the measured power factor curve with residual errors of 0.03 for first order, 0.001 for second order, 0.000130 for third order. The obtained outputs clearly indicate that the residual error decreases with the increase in polynomial order.
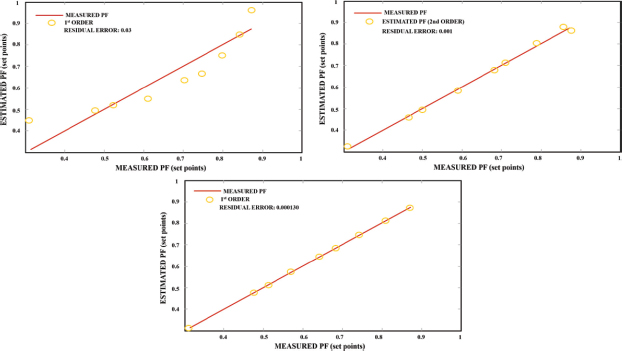
Figure 7. Residual error of (a) first order (b) second order (c) third order polynomial
The utilization of actual signals in the absence of pre-processing does not provide accurate classification. In order to achieve accurate classified results, appropriate features are extracted for fault detection. The outputs rely on the extracted features’ quality and hence in this approach, feature learning as well as classification are combined together by DBN to improve the efficiency of fault detection in induction motors. FFT is exploited for the extraction of appropriate features which are further subjected to classification. The training of DBN is carried out utilizing mean square error as the measurement of performance calculation. An improved performance of 0.00262 is obtained with the consideration of 200 epochs as shown in Figure 8.
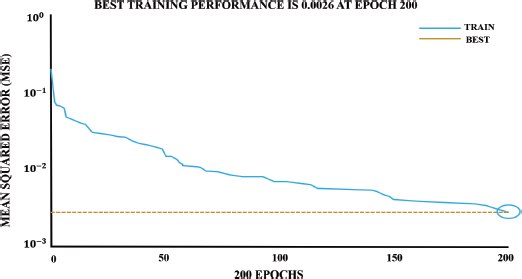
Figure 8. Training of DBN
Figure 9 indicates the Receiver Operation Characteristic (ROC) curve of validation and testing. The obtained lines for each fault reaches 1 and this indicates reduced false positive rate with increased system accuracy. Figure 10 (a) indicates the accuracy and 10 (b) indicates the loss of the proposed system. The rate of accuracy increases with the epoch and attains an increased value of 99.5%. The choice of epoch is regarded as a crucial factor because it generates a critical point at which overfitting of network to training data occurs.
Figure 9. ROC curves of validation and testing
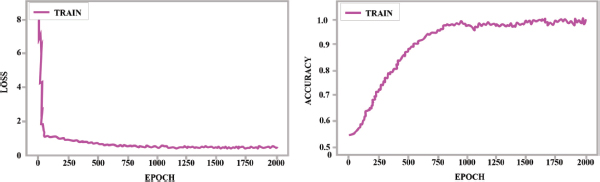
Figure 10. DBN training curve (a) Loss (b) Accuracy
Table 1 indicates the classification report of the test dataset which clearly indicates that the proposed DBN performs efficacious extraction and learning of features from the dataset. It performs efficient classification of healthy state, stator and rotor friction, bearing axis deviation, poor insulation, bearing noise and rotor aluminium end ring break. The performance of the proposed fault identification model has been analysed on the basis of sensitivity, precision, recall and F1 score.Moreover, the assessment of the aforementioned factors helps to find the industrial applicability of the proposed model.
Table 1. Test dataset classification report
Class |
FI Score |
Precision |
Recall |
Sensitivity |
Healthy |
1.00 |
1.00 |
1.00 |
1.00 |
Stator and rotor friction |
0.96 |
0.95 |
0.97 |
0.95 |
Bearing axis deviation |
0.94 |
0.97 |
0.96 |
0.94 |
Poor insulation |
0.95 |
0.96 |
0.89 |
0.90 |
Bearing noise |
0.96 |
0.93 |
1.00 |
0.95 |
Rotor aluminium end ring break |
1.00 |
1.00 |
1.00 |
1.00 |
Table 2 represents a comparison of performance measures such as mean absolute percentage error (MAPE), root mean square error (RMSE), mean absolute error (MAE) and normalized absolute error (NAE) of Support Vector Regression (SVR) and Back propagation (BP) with DBN. The proposed DBN based approach generated reduced values of error and is highly advantageous when compared to other existing approaches.
Table 2. Performance measure comparison
Approach |
MAPE |
RMSE |
MAE |
NAE |
SVR |
1.032 |
0.016 |
0.010 |
0.015 |
BP |
1.583 |
0.028 |
0.016 |
0.018 |
DBN |
0.928 |
0.015 |
0.009 |
0.010 |
Figure 11 represents the comparison of training error of the proposed DBN with other existing approaches such as SVR and BP. The proposed DBN is found to be more efficient with reduced training error when compared to other approaches.
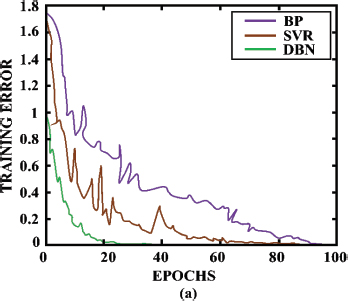
Figure 11. Comparison of training error
Figure 12 indicates the comparison of overall accuracy of the proposed DBN with other existing classifiers such as K-nearest neighbour, Multi-layer perceptron and support vector machine. The comparative reveals that the proposed approach generated improved classification results when compared to other approaches with an accuracy of 99.5%.
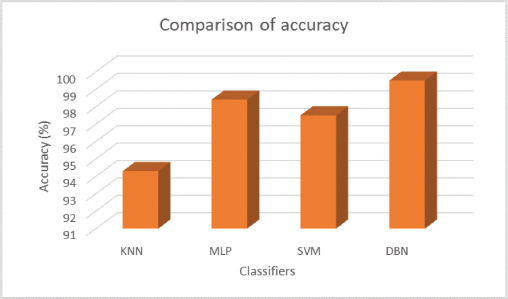
Figure 12. Comparison of accuracy
5. Conclusions
A novel approach based on deep learning has benn proposed for the mitigation of losses and fault diagnosis in induction motors. It applies regression based analysis and adopts DBN for the efficient detection of faults. DBN is formed by the stacking of RBM units one over the other. FFT is utilized for the conversion of input time domain signals to frequency domain which is further trained by DBN. The proposed approach minimizes the training error as well as enhances the accuracy of classification with the learning of multiple representation layers.The Obtained simulation results show that the deep learning based DBN is efficient in the detection of induction motor faults and generates an accuracy of 99.5%. Thus, the proposed approach generates improved classification results when compared to other traditional approaches. Future work related to the proposed approach may concentrate on the issue of overfitting. This in turn can lead to greater improvements in the performance of the DBN model in the diagnosis of faults.
5.1. Conflict of interest
The authors have no conflict of interest in publishing this work.
5.2. Plagiarism
The work described has not been published previously (except in the form of an abstract or as part of a published lecture or academic thesis), and is not under consideration for publication elsewhere. No article with the same content will be submitted for publication elsewhere while it is under review by ADCAIJ, that its publication is approved by all authors and tacitly or explicitly by the responsible authorities where the work was carried out, and that, if accepted, it will not be published elsewhere in the same form, in English or in any other language, without the written consent of the copyright-holder.
5.3. Contributors
All authors have materially participated in the research and article preparation. All authors have approved the final article to be true.
References
Abid Ben, F., Sallem, M., and Braham, A., 2019. Robust interpretable deep learning for intelligent fault diagnosis of induction motors, IEEE Transactions on Instrumentation and Measurement, Vol: 69, No: 6, pp: 3506–3515.
Ali Zawad, M., Shabbir, M. N. S. K., Liang, X., Zhang, Y., and Hu T., 2019. Machine learning-based fault diagnosis for single-and multi-faults in induction motors using measured stator currents and vibration signals. IEEE Transactions on Industry Applications, Vol: 55, No: 3, pp: 2378–2391.
Amaize, P., Ignatius, K. O., Oluwasogo, E. S., Alayande, A. S., and Airoboman, A. E., 2017. Influence of power quality problem on the performance of an induction motor. American Journal of Electrical Power and Energy Systems, Vol: 4, No:4, pp: 39–44.
Bessous, N., Zouzou, S. E., Bentrah, W., Sbaa, S., and Sahraoui, M., 2018. Diagnosis of bearing defects in induction motors using discrete wavelet transform. International Journal of System Assurance Engineering and Management, Vol: 9, No: 2, pp: 335–343.
Chouhan, A., Gangsar, P., Porwal, R., Mechefske, C. K., 2021. Artificial neural network–based fault diagnosis for induction motors under similar, interpolated and extrapolated operating conditions. Noise & Vibration Worldwide, Vol: 52, No: 10, pp. 323–33.
Ding, Xiaoxi, and He, Q., 2017. Energy-fluctuated multiscale feature learning with deep convnet for intelligent spindle bearing fault diagnosis. IEEE Transactions on Instrumentation and Measurement, Vol: 66, No: 8, pp: 1926–1935.
Dong, Shaojiang, Xu, X., and Chen, R., 2016. Application of fuzzy C-means method and classification model of optimized K-nearest neighbor for fault diagnosis of bearing. Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol: 38, No: 8, pp: 2255–2263.
Donolo, Pablo D., Pezzani, C. M., Bossio, G. R., Angelo, C. H. D., and Donolo, M. A., 2020. Derating of induction motors due to power quality issues considering the motor efficiency class. IEEE Transactions on Industry Applications, Vol: 56, No: 2, pp: 961–969.
Ghaseminezhad, Morteza, Doroudi, A., Hosseinian, S. H., and Jalilian, A., 2017. Analysis of voltage fluctuation impact on induction motors by an innovative equivalent circuit considering the speed changes. IET Generation, Transmission & Distribution, Vol: 11, No: 2, pp: 512–519.
Ghods, Amirhossein, and Lee, H., 2016. Probabilistic frequency-domain discrete wavelet transform for better detection of bearing faults in induction motors. Neurocomputing, Vol: 188, pp: 206–216.
Hassan, Ola., E., Amer, M., Ahmed, K., Abdelsalam, and Williams, B. W., 2018. Induction motor broken rotor bar fault detection techniques based on fault signature analysis–a review. IET Electric Power Applications, Vol: 12, No: 7, pp: 895–907
Hsueh, Yu-Min, Ittangihal, V. R., Wu, W., Chang, H., and Kuo, C., 2019. Fault diagnosis system for induction motors by CNN using empirical wavelet transform. Symmetry, Vol: 11, No: 10, pp: 1212.
Ibrahim, A., Anayi, F., Packianather, M., and Alomari, O. A., 2022.New hybrid invasive weed optimization and machine learning approach for fault detection. Energies, Vol: 15, No: 4, pp. 1488.
Kumar, Prashant, and Hati, A., S., 2021. Deep convolutional neural network based on adaptive gradient optimizer for fault detection in SCIM. ISA transactions, Vol: 111, pp: 350–359.
Kumar, R. R., Cirrincione, G., Cirrincione, M., Tortella, A., and Andriollo, M., 2021. Induction Machine Fault Detection and Classification Using Non-Parametric, Statistical-Frequency Features and Shallow Neural Networks. IEEE Transactions on Energy Conversion, Vol: 36, No: 2, pp. 1070–1080.
Liu, Yiqi, and Bazzi, A. M., 2017. A review and comparison of fault detection and diagnosis methods for squirrel-cage induction motors: State of the art. ISA transactions, Vol: 70, pp: 400–409.
Ma, Suliang, Chen, M., Wu, J., Wang, Y., Jia, B., and Jiang, Y., 2018. High-voltage circuit breaker fault diagnosis using a hybrid feature transformation approach based on random forest and stacked autoencoder. IEEE Transactions on Industrial Electronics, Vol: 66, No: 12, pp: 9777–9788.
Toma, N., Rafia, and Kim, J., 2020. Bearing fault classification of induction motors using discrete wavelet transform and ensemble machine learning algorithms. Applied Sciences, Vol: 10, No: 15, pp: 5251.
Pandarakone Esakimuthu, S., Mizuno, Y., and Nakamura, H., 2016. Distinct fault analysis of induction motor bearing using frequency spectrum determination and support vector machine. IEEE Transactions on Industry Applications, Vol: 53, No: 3, pp: 3049–3056.
Su, Jinya, and Chen, W., 2017. Model-based fault diagnosis system verification using reachability analysis. IEEE Transactions on Systems, Man, and Cybernetics: Systems, Vol: 49, No: 4: 742–751.
Toma Nishat, R., Prosvirin, A. E., and Kim, J., 2020. Bearing fault diagnosis of induction motors using a genetic algorithm and machine learning classifiers. Sensors, Vol: 20, No: 7, pp: 1884.
Xu, Xiaojian, Yan, X., Sheng, C., Yuan, C., Xu, D., and Yang, J., 2017. A belief rule-based expert system for fault diagnosis of marine diesel engines. IEEE transactions on systems, man, and cybernetics: systems, Vol: 50, No: 2, pp: 656–672.
Zaman, S. M. K., and Liang, X., 2021. An Effective Induction Motor Fault Diagnosis Approach Using Graph-Based Semi-Supervised Learning. IEEE Access, Vol: 9, pp. 7471–7482.
Zhang, Dongdong, An, R., and Wu, T., 2018. Effect of voltage unbalance and distortion on the loss characteristics of three-phase cage induction motor. IET Electric Power Applications, Vol: 12, No: 2, pp: 264–270.
Zhang, Nannan, Wu, L., Yang, J., and Guan, Y., 2018. Naive bayes bearing fault diagnosis based on enhanced independence of data. Sensors, Vol: 18, No: 2, pp: 463.