
Regular Issue, Vol. 11 N. 1 (2022), 5-18
eISSN: 2255-2863
DOI: https://doi.org/10.14201/adcaij.27269
 |
ADCAIJ: Advances in Distributed Computing and Artificial Intelligence Journal
Regular Issue, Vol. 11 N. 1 (2022), 5-18 eISSN: 2255-2863 DOI: https://doi.org/10.14201/adcaij.27269 |
Predicting Financial Risk Associated to Bitcoin Investment by Deep Learning
Nahla Aljojo
College of Computer Science and Engineering, Information system and Technology Department, University of Jeddah, Jeddah, Saudi Arabia
ABSTRACT
The financial risk of investing in Bitcoin is increasing, and everyone partic-ipating in the transaction is aware of it. The rise and fall of bitcoin’s value is difficult to predict, and the system is fraught with uncertainty. As a result, this study proposed to use the «Deep learning» technique for predicting fi-nancial risk associated with bitcoin investment, that is linked to its «weighted price» on the bitcoin market’s volatility. The dataset used included Bitcoin historical data, which was acquired «at one-minute intervals» from selected exchanges of January 2012 through December 2020. The deep learning lin-ear-SVM-based technique was used to obtain an advantage in handling the high-dimensional challenges related with bitcoin-based transaction transac-tions large data volume. Four variables («High», «Low», «Close», and «Volume (BTC)».) are conceptualized to predict weighted price, in order to indi-cate if there is a propensity of financial risk over the effect of their interaction. The results of the experimental investigation show that the fi-nancial risk associated with bitcoin investing is accurately predicted. This has helped to discover engagements and disengagements with doubts linked with bitcoin investment transactions, resulting in increased confidence and trust in the system as well as the elimination of financial risk. Our model had a significantly greater prediction accuracy, demonstrating the utility of deep learning systems in detecting financial problems related to digital currency.
KEYWORD
bitcoin; bitcoin in-vestment; financial risk; deep learning
1. Introduction
Risks are connected with anything that humans do, and financial risk is related with businesses whose underpinning operations are not clearly defined or involve complicated processes. When processing events becomes complicated, a dimension is required to fix the problem. As a result, a variety of tools are necessary to comprehend a complex situation or process. «Digital currency,» «Blockchain technology,» and «Deep learning» are the current study index terms. Digital currency is a type of record on a computer system that is linked to currency values. That is, it involves creating a monetary-valued representation that can be processed and exchanged on digital computer systems, as well as used over the internet, and is expected to become a «Global digital currency» with low risk and transaction costs, and no political influence in the future (Balvers, & McDonald, 2021). Monero, Ripple, Litecoin, Cardano, and Bitcoin are among the most widely utilised digital currencies. Blockchain has been described as the cryptocurrency's backbone technology, from which digital currency arose. It increases the efficiency and quality of communication while also improving the security of transactions and data exchanges (Kowalski et al., 2021). Deep learning techniques are extremely important for financial risk prediction and classification (Gloor et al., 2020). Deep learning, often known as «Deep Neural Networks,» is a type of machine learning that allows a network to learn from unstructured data and solve hard problems (Dixit S. Silakari, 2021). The softmax layer is used as an activation function in the majority of deep learning approaches for prediction. That is why it is critical that this study take this method.
Blockchain technology has emerged as a prominent platform on which a variety of applications for various activities can be found. It is the backbone technology of bitcoin implementation; it provides a public digital ledger from which users' transactions are recorded. With bitcoin, there is no central authority involved in the transaction; the ledger used in its implementation is reproducible among network participants and is administered by a dedicated computer programme (Yaga et al., 2019). Cryptocurrencies like bitcoin have generated a surge in interest in financial engineering in recent years, with hundreds of hedge funds now actively trading in digital assets. Despite the fact that some investors consider Bitcoin to be a hedge, the fact that it is so complex raises concerns about the global economic implications of a sharp drop in Bitcoin prices. Because of the financial risk connected with online financial transactions, it is vital to develop a technique for forecasting risk associated with these transactions.
Financial risk issues are handled by a variety of instruments from an economic standpoint. For the past two decades, a Value-at-Risk (VaR) methodology has been used as the standard risk measure in order to quantify regulatory and economic capital in market risk. Unfortunately, VaR was regarded as one of the high mechanisms of the loss distribution from a statistical standpoint. It was alleged that it failed to satisfy the well-known subadditivity property and did not adequately capture tail risk (Fischer et al., 2018). Similarly, Risk-Weighted Assets (RWAs), which are used to determine how to reduce risk, have failed since changes in the model can result in significant changes (Embrechts et al., 2014). Expected Shortfall (ES) is an option that overcomes the problem of average loss while also displaying a new risk metric (Fischer et al., 2018). When financial risk is managed at the micro level, the impact on the transactional level is usually minimal. Unfortunately, the financial risk associated with online purchases is high. The evaluation of losses has been used using the AR-GARCH model for different distributions for the innovation process to reflect Bitcoin financial unusual rise and fall, for example transactions utilising bitcoin also faces a lot of drawback (Jiménez et al., 2020).
Traditionally, the cryptocurrency industry is regarded as one of the world's largest unregulated markets (Foley et al., 2019). Bitcoin's financial risk is linked to its complicated characteristics of being immaterial as an electronic system based on cryptographic entities and being within a decentralised intermediate trusted third-party (Yaga et al., 2019). It is worldwide, with no geographical boundaries, irreversible, and unchangeable, as well as having other complex characteristics. In light of the financial risks connected with investing in Bitcoin, the current study examines the risks associated with bitcoin as well as the uncertainty associated with transactions involving it. For estimating the risk of bitcoin financial transactions, a deep learning approach is applied. The decision to use deep learning is based on the need to solve high-dimensional challenges related to bitcoin transactions. By increasing the number of hidden layers in the network, deep learning minimizes the number of parameters in the network and improves prediction processing.
2. Related Work
When compared to other cryptocurrencies-based digital money, Bitcoin alone maintained the highest market share at roughly 64 percent as of 2020, with a total market valuation of about US$140 billion. With a total market capitalization of almost US$140 billion, it is also recognized as a genuine legal means of payment (Young, 2017). While cryptocurrency-based financial transactions appeal to the market and investors, they nonetheless constitute a systemic financial risk. Despite the fact that they can be viewed as a stand-alone financial instrument with no ties to stock market indices, they provide investors with a diversification option (Gil-Alana et al., 2020). Deep learning has been identified as one of the most important technologies for dealing with prediction problems in a number of studies (LeCun et al., 2015; Bengio et al., 2013). It takes advantage of developments in computing technology to analyse large amounts of data in order to uncover hidden characteristics (Bengio et al., 2013; Zhang et al., 2018). Deep learning has the potential to anticipate the behaviour of complicated data due to the inclusion of numerous hidden layers in the inherited from the regular neural network architecture. Deep learning encompasses deep belief networks (DBN), generative adversarial networks (GAN), convolutional neural networks (ConvNet), stacked auto-encoders (SAE), deep recurrent neural networks (DRNN), and other types of artificial neural networks. Deep learning has been demonstrated to be beneficial in a variety of domains, which is why it was chosen for this research.
One of the most notable previous research that employed deep learning in cryptocurrency-related domains was Lamothe-Fernández et al. (2020), who used deep recurrent convolutional neural networks to forecast Bitcoin price with the ability to estimate properly. To integrate the opinion market with price prediction for cryptocurrency trading, Lopes et al. (2017) employed Convolutional Neural Networks and Long-Short Term Memory. Spilak et al. (2018) employed a Recurrent Neural Network, Long-Short Term Memory, and Deep Multi-layer Perceptron to predict the rise and fall of Bitcoin and other cryptocurrency-based currencies. Gomenz et al. (2018) employed Deep Multilayer Perceptron networks to forecast credit card fraud, despite the fact that risk and fraud are two independent issues. A Long-Short Term Memory and Recurrent Neural Network were utilised to predict Bitcoin price, with a 52 percent accuracy and an 8 percent Root Mean Square Error (Rizwan et al., 2019). Dutta et al. (2020) estimate bitcoin values with lower error using both the Gated Recurring Unit (GRU) model and Long-Short Term Memory. Jiang et al. (2017) forecasted a financial risk model using a Recurrent Neural Network, Long-Short Term Memory, and Convolutional Neural Network. According to the paper, any cryptocurrency-based portfolio management algorithms will employ the methodology. Ji and Kim (2019) achieved a precision of 60% using a deep neural network for the Long-Short Term Memory model and a convolutional neural network for Bitcoin price prediction. In order to forecast the discovery of credit card fraud, A Long-Short Term Memory model was utilised by Roy et al. (2018). Long-Short Term Memory was employed by Jurgovsky et al. (2018) to anticipate credit card theft from transaction sequences. Felizardo et al. (2019) employed Long-Short Term Memory, WaveNets, Random Forest (RF), and Support Vector Machine to make a more accurate prediction of Bitcoino price (SVM). Convolutional Neural Networks and Deep Reinforcement Learning are used by Jiang and Liang (2017) to anticipate the price of bitcoin and other cryptocurrencies-based digital currencies. Sohony et al. (2018) employed an ensemble of Feedforward Neural Networks to predict card fraud. For bitcoin price prediction, McNally et al. (2018) employed a new approach to compare Autoregressive Integrated Moving Average (ARIMA), Bayesian optimised Recurrent Neural Network, and Long-Short Term Memory. Four performance criteria are used to assess the differences between the deep learning approaches used in this study: «sensitivity,» «specificity», «precision», «accuracy», and «Root Mean Square Error (RMSE)». Finally, Linardatos and Kotsiantis (2020) use Long-Short Term Memory and eXtreme Gradient Boosting (XGBoost) to estimate bitcoin values, with a lower Root Mean Square Error of 0.999.
3. The Proposed Deep Learning Model
Deep Learning is a sort of machine learning that consists of numerous ANN layers and is extremely successful, as previously stated. It makes data modelling easier by allowing for high-level abstraction (LeCun, 2019). There are a variety of techniques to modelling deep learning, but the «Deep Multilayer Perceptron (DMLP)» is the one employed in this research. This is the first ANN-based model to be suggested, and it has the same input, output, and hidden layers as a traditional Multilayer Perceptron (MLP) model. The number of hidden layers in DMLP is more than in MLP, which is what distinguishes it from MLP (see Figure 1). The hidden layer is the governing variable when the model is run, and it contains «neurons», also known as «Perceptrons», which are the layer's key properties. Every neuron in the model's hidden layers has an input represented as «x», as well as a weight «w» and a bias «b» that are all represented as numbers. Hence, as a linear function the weight and bias is added and the output of a neuron in the neural network is illustrated in Equation (1)
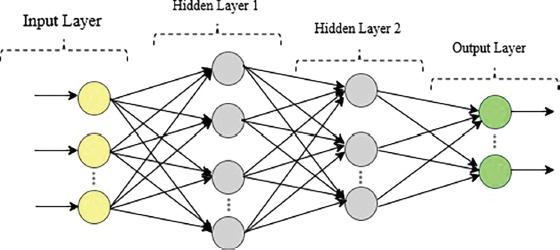
Figure 1. Deep multi-layer neural network
In a non-linear presentation with activation function, the output of each neuron is produced as the combined effect of the weighted inputs from the neurons in the preceding layer with the activation function for each neuron. There are many activation function, among which are: hyperbolic tangent, leaky ReLU, Sigmoid, swish, Rectified Linear Unit (ReLU), and softmax. Sigmoid is one of the most preferred nonlinear activation functions presented as:
thus, applying the activation function, the output associated with each perceptron is given as:
Based on the promise of deep learning for a very complicated scenario, this study used a different strategy and used softmax, which is similar to a scheme used to construct Bitcoin price prediction models. The level of relevance of the variables utilised in the prediction in the realisation of the task of feature selection is determined by deep learning linear support vector machines. (Ji & Kim, 2019).
SVMs are being used in this work as a way to improve the deep learning model. This is usually accomplished by substituting a linear support vector machine for the softmax layer of the neural network. It is now conceivable to employ the softmax in this study since it tries to resolve the financial risk associated with complex dimensional digital blockchain-currency transactions utilising deep learning techniques. Typically, given a set of nodes, the softmax layer, indicated by, offers a distribution for all of the entries. Assume that is the activation of the layer within the nodes, that is the weight connecting the layer within the nodes to the softmax layer, and that is the total input into a softmax layer is given by «a», is then considering adopting the sottmax as the activation function within nodes, it will be resolved as
Therefore, the predicted class that will replacing the softmax layer of the neural network in order to allow for the use of deep learning linear support vector machine is where and the SVM will be associated with all the nodes in the model. That if are the training data and its corresponding learning constrained for optimization, then SVM will be optimized using Equation (5).
where are slack variables, the features which penalizes the observation of the data points that do not meet or violate the margin requirements. Therefore, the corresponding unconstrained optimization problem can be defined as:
In the case of working with 10 classes in the softmax layer, it can be presented in equation 4, by replacing n with 10. Equation 6 is in primal form problem of linear SVM because that is its objective and since linear- SVM is not differentiable, the best option is the use of a popular variation known as the Deep learning linear-SVM which minimizes the squared hinge loss as shown in Equation (7):
Deep learning linear-SVM is now differentiable, however it is with both quadratic and linear expression for which it can predict the class label of a test data x with having a This means that for Kernel SVMs, optimization must be performed in the dual. It is quite necessary to avoid the problem of scalability that is associated with Kernel SVMs. That is why adopting linear SVMs with standard deep learning models is crucial. However in extending SVMs for multiclass problems «k», it is appropriate to initiate k class problems so that k linear SVMs will be trained independently, that is the output of the k−th SVM will be and the predicted class is Then considering that the target of Deep learning linear-SVM is to train deep neural networks for prediction, as a result, this current study utilizes the lower layer weights of the model to be learned by back propagating the gradients from the top layer linear SVM. That is why the objective functions of the SVM is differentiated with respect to the activation of the penultimate layer, hence the differentiation of the activation with respect to the penultimate layer and changing the input x with the penultimate activation q is given by Equation (8),
Where is the indicator function. Likewise, for the Deep learning linear-SVM, we have Equation
4. Experimental Analysis and Evaluation Technique
The experimental analysis and evaluation of the results involves pre-processing, and the final analysis. The Deep learning linear-SVM were used to predict «Financial risk attempts» based on the dataset obtained at Kaggle «https://www.kaggle.com/mczielinski/bitcoin-historical-data» for the «Bitcoin Historical Data, that is the Bitcoin data at 1-minutes intervals from select exchanges, Jan 2012 to Dec 2020 containing «Timestamp», «Open», «High», «Low», «Close», «Volume_(BTC)», «Volume_(Currency)», «Weighted_Price» in 2841377 rows and 7 columns and then these data are normalized. The normalization involves transformation of data in the stage called data pre-processing step where raw data sources are scaled to the range of values within a uniform scale to improve the quality of the data so that the prediction accuracy can be improved. Even though the efficacy of data normalization was questioned following the fact that it might destroy the structure in the original (raw) data, Abubakar et al. (2015) addressed that comparing the prediction performances of multilayer perceptron neural network model built with normalized and raw data respectively, in which it was reveals that the model built on normalized data significantly outperformed the one with raw data. Therefore, the nonnumeric label features were all converted into numeric forms. furthermore, the unrelated features such as «Timestamp» and «open» were removed. Then Furthermore, «High», «Low», «Close», «Volume_(BTC)», «Volume_(Currency)», are set as the observed values of features to have a length of 1, while «Weighted_Price» is the label. Thereafter, the normalized data are partitioned into various ratios of training and testing until a desirable partition were found. Following the setup presented in section 2, the SVM and deep learning models were established based on the training data. Thereafter, the models were tested with the test data followed by the performance evaluation of models.
Finally, the evaluation of the model will follow by using the sensitivity and specificity measures. Considering that substantial research studies on prediction utilized rules-based scores, sensitivity and specificity in identifying and predicting problems. The sensitivity-based approach reveals the tries each network weight or node's contribution and the least effect on the objective function. Hence, the positive and negative class of performance measure present true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN). TP: precisely predict, FP: erroneously predict, FN: erroneously rejected, TN: precisely rejected. This is used for measuring the «Sensitivity (Se)», and «Specificity(Sp)», based on the following evaluates the performance measure of the models used:
• Se = True positive rate = Recall = TP/ (TP + FN)
• Sp = True negative rate = TN/ (TN + FP)
• Prevalence = (TP + FP) / (TP+TN+FP+FN)
• Positive predictive value = (Se * Prevalence)/({( Se * Prevalence)+(1- Sp)*(1-Prevalence)})
• Negative predictive value = (Sp * (1-Prevalence))/({(1- Se)* Prevalence)}+{(Sp)*(1-Prevalence)})
• Detection rate = TP / (TP+TN+FP+FN)
• Detection Prevalence = (TP +FN) / (TP+TN+FP+FN)
• Balance Accuracy = (Se + Sp) / 2
The processing stage of the analysis implement Deep learning linear-SVM on various hidden layers of 5, 6 and 7 and each layer include the different number of neurons ranging from 200, 170, 150, 100, 50, 20 and 5 respectively. This is where the softmax activation layer of the neural network is replaced with a linear support vector machine. This study selected optimum numbers based on the model’s accuracy, that is all features were used. The computer system used for this experiment is equipped with Intel® Core™ i7-10750H CPU @5.0 GHz, and 16 GB Ram capacity.
5. Presentation of The Findings
There were 2841377 Bitcoin Historical Data gathered, but 680054 records are missing data. These datasets were split into training and testing dataset with various percentage ratios. Series of analysis were carried out. The performance of the prediction model for the first partition 80:20 performed on three different «Fitted ROC Area» reveals 0.75; 0.853; 0.893 (see Figure 2) respectively, this is used to understand the performance of the model. The model's accuracy was 95.2%, where the 95% confidence interval was 0.944-0.962. The sensitivity and specificity of the model were 0.9910 and 0.1810, respectively. was 0.8731. The accuracy of the model was found to be 91.27%, where the 95% confidence interval was 0.9219-0.9411. The sensitivity and specificity of the model were 0.8310 and 0.1221, respectively.
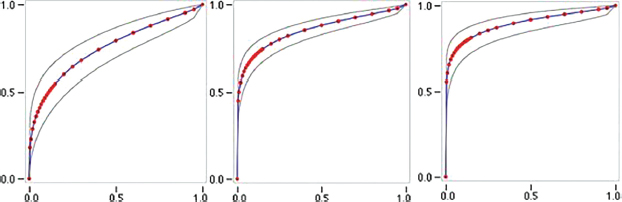
Figure 2. The Fitted ROC Area in the First Experimental Scenario
On further analysis using 70:30 partitions ratio, the model was tested and the prediction model perfor-mance was 0.905; 0.935; 0.949 respectively, the last «Fitted ROC Area» accuracy was 94.10%, at 95% confidence interval within 0.9101-0.9420. The sensitivity and specificity of the model were 0.9910 and 0.1813, respectively (see Figure 3).
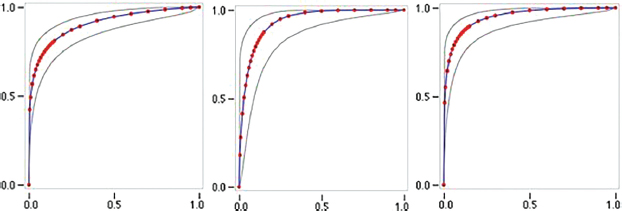
Figure 3. The Fitted ROC Area in the Second Experimental Scenario
The analysis of the next partition is with 60:40 ratio shows that the prediction models The next round of the analysis with same dataset used both ANN-based and SVM-based prediction model. The performance of the prediction model under the «Fitted ROC Area» r is 0.951; 0.952; 0.974 respectively and at the best partition, under at 95% confidence interval was 0.9019 – 0.9101, where the sensitivity and specificity of the model were 0.9791 and 0.1721 (see Figure 4).
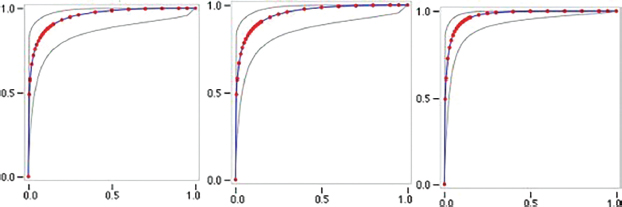
Figure 4. The Fitted ROC Area in the Third Experimental Scenario
Further analysis of the prediction rate and prevalence was found to be lower than the Deep learning linear-SVM-based prediction model. Similarly, in the 70:30 and 90:10 partition analysis, the performance under the «Fitted ROC Area» was 0.9631 and 0.95254 respectively. It is also reveals that 92.62% and 94.37 accuracies were obtained from the model respectively.
Since the Deep learning linear-SVM-based prediction model proven to be a good model, further analysis was developed a model for those explanatory variables and test their significance. The bitcoin historical dataset analyzed based on «Timestamp», «Open», «High», «Low», «Close», «Volume_(BTC)», and «Volume_(Currency)», relation to «Weighted_Price» draw a lot of conclusion. For this study, it is focus toward understanding risk associated with those looking for the impact of weighted price. That is when investors forecast rise of price and suddenly leads to a risk. That means what if at the time investors predict rise of bitcoin price leads to a financial lost if the price does not rise, and vice versa. The Deep learning linear-SVM-based prediction model was able to shows that the variables used predict the weighted price at good prediction performance as explained earlier on. Now in order to further validate the model, the effect of the explanatory variables and test their significance has been evaluated (see Table 1).
Table 1. The Effect of Explanatory Variables and Significance
Variable |
β-coefficient |
HR |
Z-value |
P-value |
Timestamp |
0.0871 |
1.2121 |
0.53 |
0.7112 |
Open |
0.3051 |
2.1281 |
3.20 |
0.0019 |
High |
0.4118 |
1.7124 |
2.91 |
0.0128 |
Low |
0.1817 |
1.3134 |
0.81 |
0.5321 |
Close |
-0.0541 |
0.8179 |
-1.93 |
0.0061 |
Volume_(BTC) |
0.5213 |
1.6542 |
2.62 |
0.0017 |
Volume of bitcoin digital currency (Volume_(BTC)) was significant with p-value = 0.0017, and make the highest contribution of 52%. It means the more the volume of bitcoin, the more the weighted prices on its trading volume responded worldwide and increase. This is followed by the state bitcoin unit when it gets high. The result was revealed that the bitcoin weighted price relationship with the bitcoin «unit high» is significant at 0.0128, and there is 41% prediction weight associated to the impact of «high unit» value of bitcoin. This is also related to the «open unit value» of bitcoin over time, where it is significant at 0.0019, and has 30% impact on bitcoin weighted price. The low unit value of bitcoin does not have a significant impact of weighted price. This implies that when a unit of bitcoin price open lows, investors rush to invest, that is, changes in the unit value of bitcoin relatively results in increase volume of investment. However, the risk will not be perceived at that moment, because the weighted price is low
Based on their prediction impact, it can be revealed from the correlation analysis that «Open», «High», «Low», «Close» and «Weighted price» are highly correlated and exhibit multivariate time series effect on financial risk.
6. Discussions
The use of the Deep learning linear-SVM-based prediction model in this study serves as a validation and reliability assessments of the variables used for predicting financial risk on bitcoin investment. Furthermore, the impact of each variable on the model was evaluated. The logic which this paper dwells, lies with establishing the impact of bitcoin investment towards financial risk. That is, what are the financial risk associated with the key explanatory criteria on bitcoin and what is the risk indicator among the criteria. There are many studies that were concern with prediction of bitcoin future price, but ignore how the price can be associated to financial risk (Lamothe-Fernández et al., 2020; Lopes et al., 2017). That is why this study formulate financial risk resolution with the variables involve in investing in Bitcoin. These variables influence the rise and fall of the value of bitcoin and are so much associated with uncertainty. It involves «High unit price», «Low unit price», «Close unit price», and the «Volume of the units’ prices». These variables are used to predict weighted price, however, weather the weighted price can lead to financial risk were ignore by previous research.
Evaluation of the deep learning linear-SVM-based prediction model has produce some good prediction performance for the entire series of analysis under various partitioning of the dataset. The degree or measure of the curve indicating the prediction performance was high. The model's accuracy in all scenarios were very good, in both sensitivity and specificity. That is «High unit price», «Low unit price», «Close unit price», and the «Volume of the units’ prices» predicted the «weighted price» of the bitcoin units, that means that the model predicted that investors can expect the rise of bitcoin price at a certain time and if their expectation fails, then it leads to financial lost. Many assumptions about bitcoins of a being a real decentralized currency that follows similar transactions patterns of fiat currency is proven in the research. Although in its real implementation, to some certain extend, Bitcoin face some major drawbacks in performing most of the basic roles that fiat currency undertakes. That is transaction which was on the basis of the variables used in this research were perceived as illegal by some people because some are aware that investing in Bitcoin is risky. It is very difficult to compare Bitcoin unit value with any financial assets due to its volatility. The risk on investing can be concluded by this research to be acceptable by the investors. It’s obvious that every investor, in one way or the other belief on the risk of investing on bitcoin. What this research does different from other research understating the effects of other weighted price to the risk, and the finding reveals that only when the «Low unit price» of bitcoin over time is influencing weighted price which is consequently generating potential financial risk. That is many investors invest at a time when the price is at low unit, their rush to invest in a risk because other variables: «Close unit price», and the «Volume of the units’ prices» does have a significant influence to «weighted price» within those period.
It is also noteworthy that the mainstream financial institutions consider Bitcoin as part of risky investment, because it creates many groups of people that utilized many online platforms that are not vetted by government or any defense body which determined. Investors and the society are now at ease, their perceptions are money can be made and lost at same time. The risk of investing is different from that of stocks based on the fact that it’s a new class of investment. Analysis of the results of this study indicate that the regression analysis performed with the explanatory variables predicting weighted price indicate that some variables are significant predictors of weighted price. This means that there are benefits of investing in Bitcoin explained by the research variables. This create a new market that offers Bitcoin as a stable financial asset, and serve as an attractive tool for the investors. However, the risk of Bitcoin contributes to an inefficient collection of dynamics market characteristics.
The originality of this work as compared to previous research studies lies with the methodology (see Table 2). The methodology used in this study differs from previous research studies in that it investigates financial risk at the micro level and shows the influence on the transactional level. For example, Embrechts et al. (2014) used «Risk-Weighted Assets (RWAs)» for investigating financial risk at the micro level, and its method shows the influence on the transactional level, whereas Fischer et al. (2018) used Value-at-Risk (VaR) for financial risk analysis, but its results in a similar vein, Foley et al. (2019) employ the Expected Shortfall (ES) risk metric to tackle the problem of average loss, which was similarly not applicable to online transactions. Yaga et al. (2019) used a Lightweight node Blockchan-based Bitcoin's financial risk and demonstrated that it is connected to the fact that it is a decentralised intermediary trustworthy third-party (decentralised intermediary). A similar model, the AR-GARCH model, is used by Jiménez et al. (2020) for heterogeneous distributions, which may be able to reflect Bitcoin's distinctive development and decline, but which has numerous problems when it comes to online transactions. When applied to bitcoin investment transactions, this research's Deep Learning Linear-SVM-based model has been successful in identifying risk engagements and disengagements linked with the transactions.
Table 2. Comparison of Results with Some Previous Research Work
Risk-Weighted As-sets (RWAs) |
RWAs shows that managing financial risk at the micro level has a negligible influence on the transactional level. Online trans-actions, however, carry a significant financial risk |
|
Value-at-Risk (VaR) |
VaR capture tail financial risk but didn't meet the well-known subadditivity property for online transaction |
|
Expected Shortfall (ES) |
Expected Shortfall (ES) is a risk metric that solves the problem of average loss while also providing a new way to measure risk. |
|
Lightweight node |
Blockchan-based Bitcoin's financial risk is tied to being a de-centralised intermediary trust-worthy third-party |
|
AR-GARCH model |
While the AR-GARCH model for diverse distributions might capture Bitcoin's peculiar growth and fall, it also has many draw-backs |
|
This paper |
Deep Learning Linear-SVM-based model |
It has been possible to identify risk engagements and disengage-ments associated with bitcoin in-vestment transactions |
7. Conclusion
This study has presented an evaluation of risks associated with investing in bitcoin and the variables influencing the activities that are not clearly or involve complex process of transaction in bitcoin. Deep learning is the central part of this study, because is utilized for the modelling the prediction. The study has indicated the tendency of financial risk over the Bitcoin units. Experimental analysis was carried out, sev-eral scenarios were tested and the Deep learning linear-SVM-based prediction model used produced an important result because the performance model for the prediction of financial risk associated to bitcoin investment were very good. This finding indicated that investing in Bitcoin relies on the changes of some explanatory variables and investors are quitted aware that these variables influence financial risks over time. Considering this results, it can be concluded that transactions of bitcoin can yield benefits because investors are quite aware of the gains and if clearly understood will eliminate financial risk. That is why the study serves as an important tool for considering the potential of resolving financial risk through predicting the risks associated with Bitcoin investment. Furthermore, this study has implication on investing in Bitcoin unit price rise and fall and the uncertainty surrounding it. Weighted price has been found to be associated with the volatility of the bitcoin market because the variable is influenced by High unit price, Low unit price, Closing unit price as well as the volume of the Bitcoin over time of Bitcoin historical data. Finally, the study contributed in clearing doubts associated with investing in bitcoin in order to give investors’ confidence and trust to eliminate financial risk. Our model retained substantially higher prediction accuracy, hence this highlight the potential of deep learning systems in predicting financial risks associated with digital currency.
References
Abubakar, A.I., Chiroma, H. and Abdulkareem, S., 2015. Comparing performances of neural network models built through transformed and original data. In 2015 International Conference on Computer, Communications, and Control Technology (I4CT) (pp. 364–369).
Balvers, R.J. and McDonald, B., 2021. Designing a global digital currency. Journal of International Money and Finance, 111, p.102317.
Bengio, Yoshua, Aaron Courville, and Pascal Vincent. «Representation learning: A review and new perspectives». IEEE transactions on pattern analysis and machine intelligence 35, no. 8 (2013): 1798–1828.
Dixit, P. and Silakari, S., 2021. Deep learning algorithms for cybersecurity applications: A technological and status review. Computer Science Review, 39, p.100317.
Dutta, A., Kumar, S. and Basu, M., 2020. A gated recurrent unit approach to bitcoin price prediction. Journal of Risk and Financial Management, 13(2), p.23.
Embrechts, P., Puccetti, G., Rüschendorf, L., Wang, R. and Beleraj, A., 2014. An academic response to Basel 3.5. Risks, 2(1), pp.25–48.
Felizardo, L., Oliveira, R., Del-Moral-Hernandez, E. and Cozman, F., 2019, October. Comparative study of Bitcoin price prediction using WaveNets, Recurrent Neural Networks and other Machine Learning Methods. In 2019 6th International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC) (pp. 1–6).
Fischer, M., Moser, T. and Pfeuffer, M., 2018. A discussion on recent risk measures with application to credit risk: Calculating risk contributions and identifying risk concentrations. Risks, 6(4), p.142.
Foley, S., Karlsen, J.R. and Putniņš, T.J., 2019. Sex, drugs, and bitcoin: How much illegal activity is financed through cryptocurrencies?. The Review of Financial Studies, 32(5), pp.1798–1853.
Gil-Alana, L.A., Abakah, E.J.A. and Rojo, M.F.R., 2020. Cryptocurrencies and stock market indices. Are they related?. Research in International Business and Finance, 51, p.101063.
Gloor, P., Colladon, A.F., de Oliveira, J.M. and Rovelli, P., 2020. Put your money where your mouth is: Using deep learning to identify consumer tribes from word usage. International Journal of Information Management, 51, p.101924.
Gómez, J.A., Arévalo, J., Paredes, R. and Nin, J., 2018. End-to-end neural network architecture for fraud scoring in card payments. Pattern Recognition Letters, 105, pp.175–181.
Ji, S., Kim, J. and Im, H., 2019. A comparative study of bitcoin price prediction using deep learning. Mathematics, 7(10), p.898.
Jiang, Z. and Liang, J., 2017. Cryptocurrency portfolio management with deep reinforcement learning. In 2017 Intelligent Systems Conference (IntelliSys) (pp. 905–913).
Jiang, Z., Xu, D. and Liang, J., 2017. A deep reinforcement learning framework for the financial portfolio management problem. arXiv preprint arXiv:1706.10059.
Jiménez, I., Mora-Valencia, A. and Perote, J., 2020. Risk quantification and validation for Bitcoin. Operations Research Letters, 48(4), pp.534–541.
Jurgovsky, J., Granitzer, M., Ziegler, K., Calabretto, S., Portier, P.E., He-Guelton, L. and Caelen, O., 2018. Sequence classification for credit-card fraud detection. Expert Systems with Applications, 100, pp.234–245.
Kowalski, M., Lee, Z.W. and Chan, T.K., 2021. Blockchain technology and trust relationships in trade finance. Technological Forecasting and Social Change, 166, p.120641.
Lamothe-Fernández, P., Alaminos, D., Lamothe-López, P. and Fernández-Gámez, M.A., 2020. Deep Learning Methods for Modeling Bitcoin Price. Mathematics, 8(8), p.1245.
LeCun, Y., 2019. 1.1 deep learning hardware: Past, present, and future. In 2019 IEEE International Solid-State Circuits Conference-(ISSCC) (pp. 12–19).
LeCun, Y., Bengio, Y. and Hinton, G., 2015. Deep learning. nature 521 (7553), 436–444.
Linardatos, p. and Kotsiantis, S., 2020. Bitcoin Price Prediction Combining Data and Text Mining. In Advances in Integrations of Intelligent Methods (pp. 49–63). Springer, Singapore.
Lopes, R.G., Fenu, S. and Starner, T., 2017. Data-free knowledge distillation for deep neural networks. arXiv preprint arXiv:1710.07535.
McNally, S., Roche, J. and Caton, S., 2018. Predicting the price of bitcoin using machine learning. In 2018 26th euromicro international conference on parallel, distributed and network-based processing (PDP) (pp. 339–343).
Rizwan, M., Narejo, S., and Javed, M., 2019. Bitcoin price prediction using deep learning algorithm. In 2019 13th IEEE. International Conference on Mathematics, Actuarial Science, Computer Science and Statistics (MACS) (pp. 1-7) .
Roy, A., Sun, J., Mahoney, R., Alonzi, L., Adams, S. and Beling, P., 2018. Deep learning detecting fraud in credit card transactions. In 2018 Systems and Information Engineering Design Symposium (SIEDS) (pp. 129–134).
Sohony, I., Pratap, R. and Nambiar, U., 2018, January. Ensemble learning for credit card fraud detection. In Proceedings of the ACM India Joint International Conference on Data Science and Management of Data (pp. 289–294).
Spilak, B., 2018. Deep neural networks for cryptocurrencies price prediction (Master's thesis, Humboldt-Universität zu Berlin).
Yaga, D., Mell, p., Roby, N. and Scarfone, K., 2019. Blockchain technology overview.arXiv preprint arXiv:1906.11078.
Young, C., 2017. South Korea Officially Legalizes Bitcoin, Huge Market for Traders. Available online: https://cointelegraph.com/news/south-korea-officially-legalizes-bitcoin-huge-market-fortraders (accessed on 02 May 2020).
Zhang, C., Tan, K.C., Li, H. and Hong, G.S., 2018. A cost-sensitive deep belief network for imbalanced classification. IEEE transactions on neural networks and learning systems, 30(1), pp.109–122.
Author’s Biography
Nahla ALJOJO obtained her PhD in Computing at Portsmouth University. She is currently working as Associate Professor at College of Computer Science and Engineering, Information system and information Technology Department, University of Jeddah, Jeddah, Saudi Arabia. Her research interests include: adaptivity in web-based educational systems, e-Business, leadership’s studies, information security and data integrity, e-Learning, education, machine learning, health informatics, environment and ecology, and logistics and supply chain management. Her contributions have been published in prestigious peer-reviewed journals.